Max-Planck-Institut für Meteorologie: Warum ist das Klima stochastisch?

Eine Zeitreihe einer Klimavariablen ähnelt oft einer zufälligen Abfolge. Diese scheinbare Zufälligkeit wird im Allgemeinen auf die unberechenbare und chaotische Natur dynamischer Systeme zurückgeführt. Bislang gibt es keine Theorie darüber, wie ein Klimamodell als rein deterministisches dynamisches System zufällige Lösungen erzeugen kann. In einer kürzlich erschienenen Veröffentlichung zeigt Jin-Song von Storch, dass Zufälligkeit und damit Irreversibilität in Lösungen eines rein deterministischen dynamischen Systems aus einer bisher unbekannten Dissipation resultieren.

Ein Klimamodell stellt ein dynamisches System dar, dessen Zustand durch einen Satz von Modellvariablen beschrieben wird. Die zeitliche Entwicklung dieses Zustands kann entweder in Form von Differentialgleichungen oder in Form von Lösungen, die man durch vorwärts Integration dieser Gleichungen erhält, beschrieben werden. Während bei ersterem die „Geschwindigkeit“ der Veränderung der betrachteten Variablen im Vordergrund steht, geht es bei letzterem um die „Position“ der Variablen, die nach einer bestimmten Zeitspanne erreicht wird. Der Klarheit halber wird die Funktion, die die „Geschwindigkeit“ bestimmt, als Differentialkraft F bezeichnet, und die Funktion, die die nach einer Zeitspanne der Länge T erreichte „Position“ bestimmt, als Integralkraft G_T. Ob eine Lösung zufällig ist, so dass die „Positionen“ zu zwei Zeitpunkten, die durch ein Zeitintervall der Länge T getrennt sind, unabhängig voneinander sind, wird allein durch die Integralkraft G_T bestimmt.

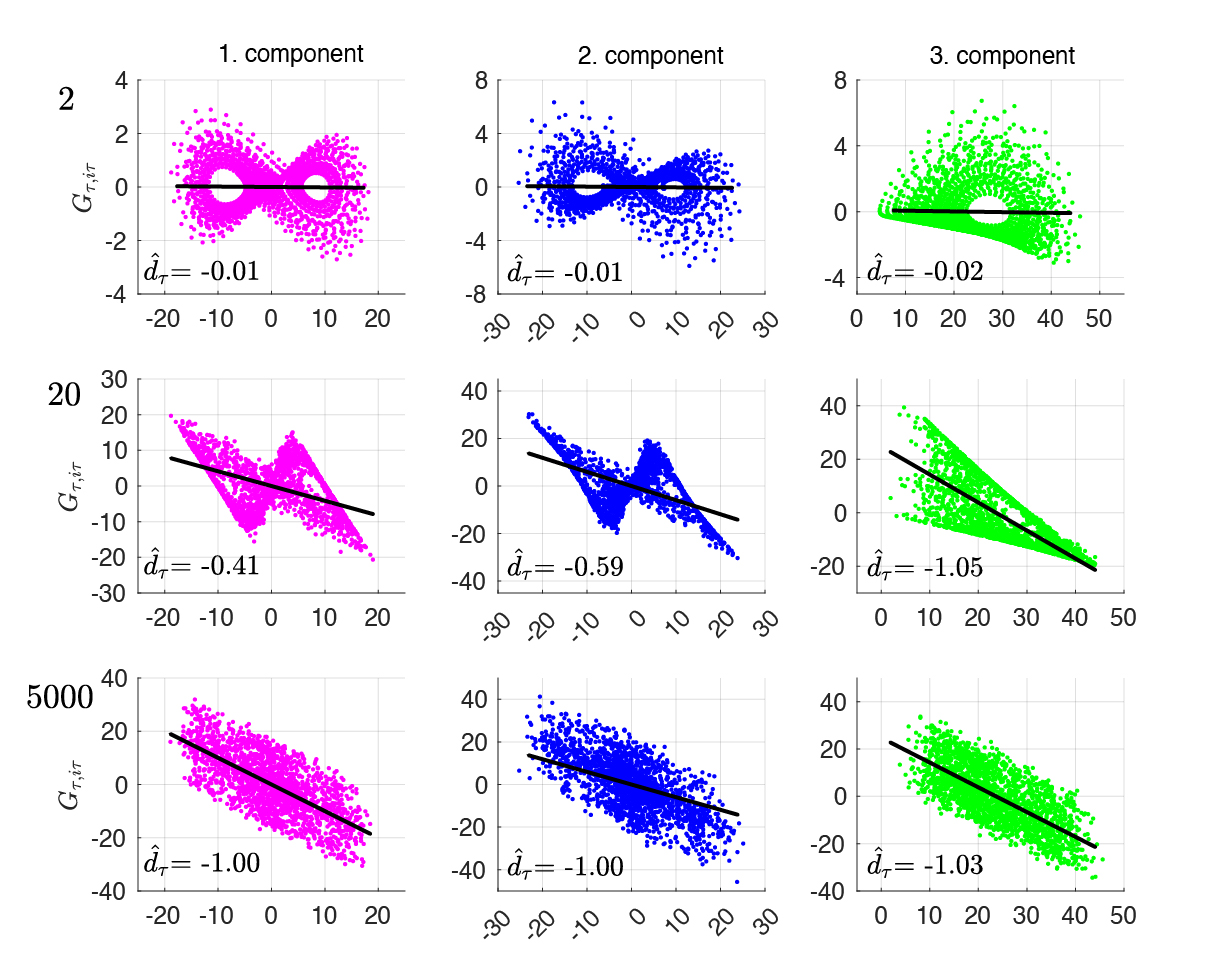
Abbildung: Dissipation in G — Dissipation in G, dargestellt durch die negativen Steigungen (schwarze Linien), die durch Regression der Integralkraft G von der Variablen x gegen x erhalten und durch die negativen Werte von d quantifiziert werden (Zahlen in jedem Diagramm). Diese Dissipation besteht unabhängig von den betrachteten Variablen (durch verschiedene Farben gekennzeichnet) und der Länge der Integrationsperiode T (in verschiedenen Reihen betrachtet, wobei die oberste der kürzesten und die unterste der längsten Integrationsperiode entspricht). Credit: von Storch

Jin-Song von Storch postuliert, dass die Integralkraft G_T Eigenschaften hat, die die Differentialkraft F nicht hat. G_T enthält insbesondere eine Dissipation. Diese Dissipation ist durch einen negativen Faktor d gekennzeichnet. Das heißt, dass nur ein Teil der Variablen zum Anfangszeitpunkt t, nämlich (1+d), von der Variablen zu einem späteren Zeitpunkt t+T beibehalten wird. Für ein ausreichend großes T erreicht die Dissipation ihre maximale Stärke, gekennzeichnet durch d = -1. Mit d = -1 „löscht“ die Dissipation in G_T die Verbindung der Variablen zum Zeitpunkt t+T mit der Variablen zum Zeitpunkt t vollständig. Die Lösung dieser Variablen an den durch T getrennten Zeitpunkten ist unabhängig voneinander und zufällig. Außerdem ist sie irreversibel, was bedeutet, dass die Variable am vergangenen Zeitpunkt t nicht aus der Variablen am zukünftigen Zeitpunkt t+T gewonnen werden kann. Die Dissipation in G_T ist nicht und kann nicht Teil der bekannten Dynamik, die durch F dargestellt wird. Daher kann die Lösung eines dynamischen Systems zufällig sein, trotz der rein deterministischen Natur von F. Jin-Song von Storch überprüft diese Postulate anhand des Lorenz-Modells von 1963, einem Paradebeispiel deterministischer chaotischer Systeme.

Aus physikalischer Sicht lässt sich festhalten, dass Dissipation in G_T das Resultat aktiver Wechselwirkungen zwischen Modellvariablen ist, die innerhalb eines Zeitraums der Länge T abgeschlossen wurden. Diese Dissipation existiert ausschließlich in mehrdimensionalen dynamischen Systemen. Die Stärke der Dissipation hängt von der Anzahl der Freiheitsgrade des betrachteten Systems ab, die maßgeblich durch die Anzahl der Gitterpunkte des Klimamodells bestimmt wird. Es muss untersucht werden, ob eine solche Abhängigkeit besteht und wie sich diese auf das von einem Klimamodell mit unterschiedlichen Auflösungen simulierte Klima auswirkt.

Originalveröffentlichung

von Storch, J.-S. (2024) ‘Randomness and Integral Forcing’, Tellus A: Dynamic Meteorology and Oceanography, 76(1), p. 74–89. doi.org/10.16993/tellusa.4065.

Kontakt

Dr. Jin-Song von Storch
Max-Planck-Institut für Meteorologie
jin-song.von.storch@mpimet.mpg.de

Back