Max-Planck-Institute for Meteorology: Why is climate stochastic?

A time series of a climate variable often resembles a random sequence. This apparent randomness is generally attributed to the unpredictable and chaotic nature of dynamical systems. So far, there exists no theory about how a climate model, as such a purely deterministic dynamical system, can produce random solutions. In a recent publication, Jin-Song von Storch shows that randomness, and with that irreversibility, in solutions of a purely deterministic dynamical system emerge from a hitherto unknown dissipation.

A climate model represents a dynamical system, whose state is described by a set of model variables. The time evolution of this state can be described either in form of differential equations, or in form of solutions obtained by integrating the differential equations forward in time. While the former focuses on the “speed” of the change of the considered variable, the latter focuses on the “position” of the variable reached after a certain time period. For the sake of clarity, the function that determines the “speed” is referred to as the differential forcing F; and the function that determines the “position” reached after a time period of length T is referred to as the integral forcing G_T. Whether or not a solution is random, so that the “positions” at two times separated by a time interval of length T are independent of each other, is determined solely by the integral forcing G_T.

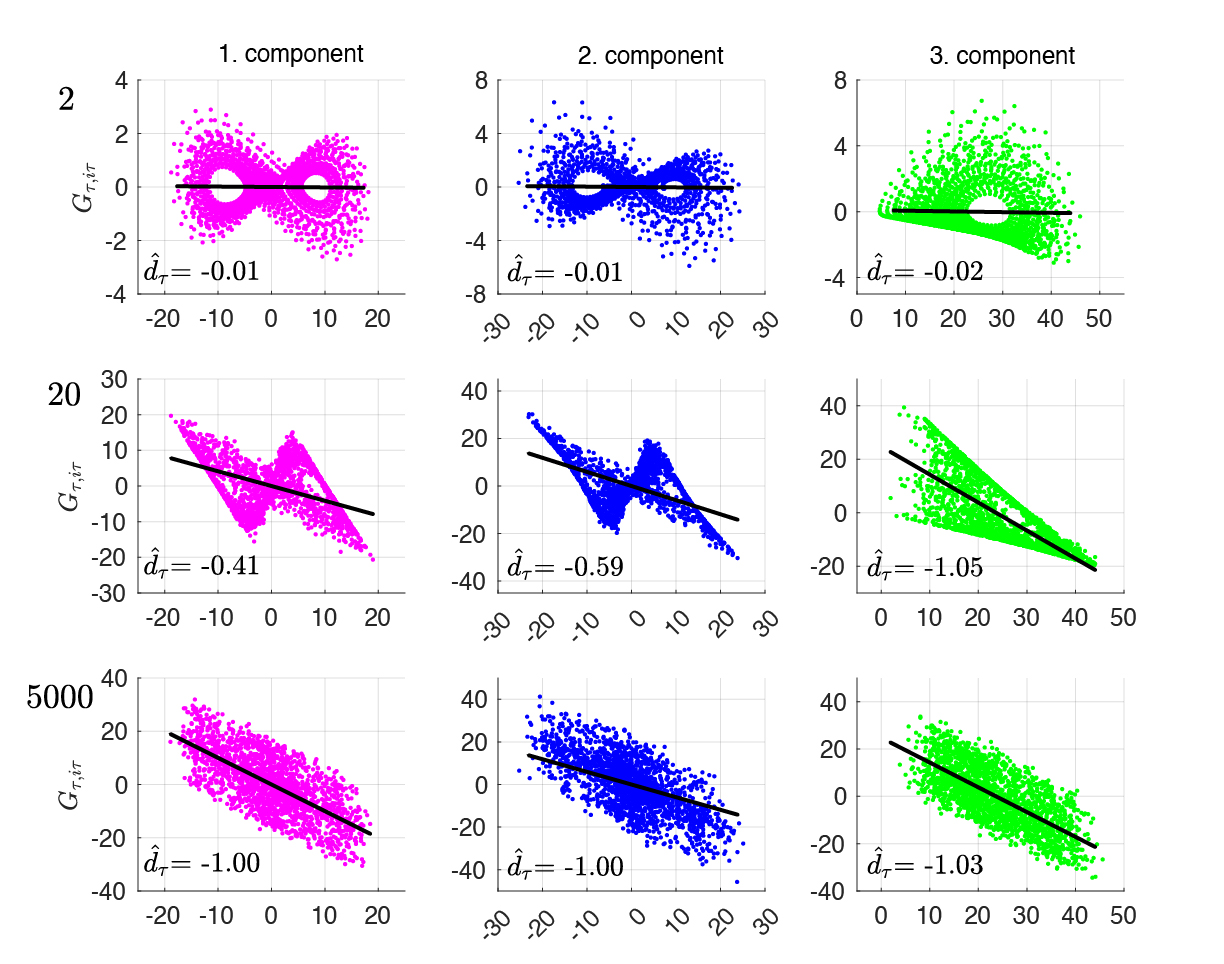
Figure: Dissipation in G — Dissipation in G, pictured by the negative slopes (black lines) obtained by regressing the integral forcing G of variable x against x and quantified by the negative values of d (numbers given in each diagram). This dissipation exists independent of the variables considered (indicated by different colors) and the length of the integration period T (considered in different rows with the top one corresponding to the shortest and the bottom one the longest integration period). Credit: von Storch

Jin-Song von Storch postulates that the integral forcing G_T has properties that the differential forcing F does not have. In particular, G_T always contains a dissipation. This dissipation is characterized a negative factor dsuch that only a portion of the variable at initial time t, namely (1+d), is retained by the variable at a later time t+T. For a sufficiently large T, the dissipation reaches its maximum strength characterized by d= -1. With d= -1, the dissipation in G_T completely “erases” the link of the variable at time t+T with the variable at time t. The solution of this variable at times separated by T becomes independent to each other, hence random; and irreversible, meaning that the variable at the past time t cannot be obtained from the variable at the future time t+T. The dissipation in G_T is not and cannot be a part of the known dynamics represented by F. Due to this dissipation, the solution of a dynamical system can be random, despite the purely deterministic nature of F. Jin-Song von Storch verifies these postulates in terms of the Lorenz’s 1963 model, a prime example of deterministic chaotic systems.

Physically, the dissipation in G_T arises from active interactions among model variables that have completed over a time period of length T. As such, this dissipation exists only for multi-dimensional dynamical systems, and the strength of this dissipation can depend on the number of degrees of freedom of the dynamical system considered (or the number of grid points of the climate model considered). It remains to be investigated whether such a dependence exists and how this dependence affects the climate simulated by a climate model at different resolutions.

Original publication

von Storch, J.-S. (2024) ‘Randomness and Integral Forcing’, Tellus A: Dynamic Meteorology and Oceanography, 76(1), p. 74–89. doi.org/10.16993/tellusa.4065.

Contact

Dr. Jin-Song von Storch
Max Planck Institute for Meteorology
jin-song.von.storch@mpimet.mpg.de

Back