
Komplexe Modellierung und extremes Computing
Unser Ziel ist es, die Dynamik des Ozeans und seine Rolle für das Klima zu verstehen, indem wir numerische Methoden, physikalische Überlegungen, mathematische Analysen und numerische Experimente kombinieren. Die Gruppe "Komplexe Modellierung und extremes Computing"
- entwickelt modernste Zirkulationsmodelle für den Ozean,
- führt Hochleistungsberechnungen durch,
- entwickelt hochentwickelte Diagnoseverfahren zur Analyse der simulierten Zirkulation.
Das Thema der Gruppe ist an der Schnittstelle zwischen angewandter Mathematik, wissenschaftlichem Rechnen und physikalischer Ozeanographie angesiedelt und konzentriert sich auf das Ozeanmodell ICON-O.
Numerik auf dem neuesten Stand der Technik
Wir entwickeln strukturerhaltende numerische Verfahren, die ein physikalisches Konzept in ein numerisches Modell einbetten. Diese Methoden, die auch als "mimetische" oder "physikalische Erfassungsmethode" bezeichnet werden, zielen darauf ab, die Qualität der Simulationen zu verbessern, indem diskrete Äquivalente wesentlicher Eigenschaften der Kontinuumsphysik formuliert werden. Diese Idee wurde beim Entwurf und der Realisierung des allgemeinen Ozeanzirkulationsmodells ICON-O mit Leben gefüllt.
Innovative Parameterisierungen
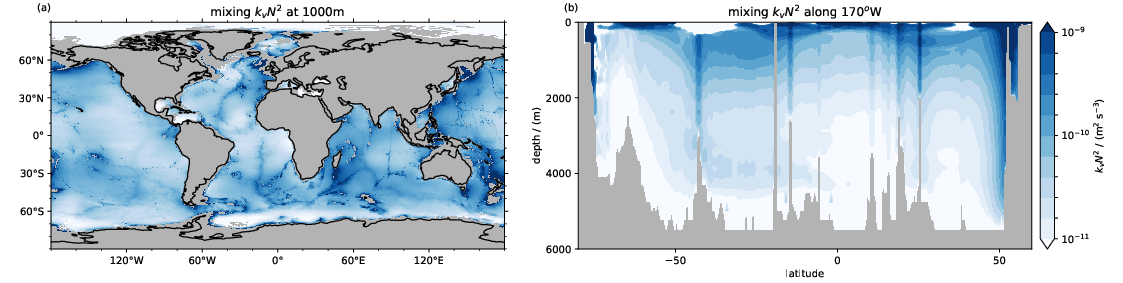
Mehrere wichtige Prozesse im Ozean bleiben ungelöst. Diese Prozesse werden in Ozeanmodellen durch Parametrisierungen oder Subgrid-Scale-Modelle dargestellt. Für die Parametrisierung der diapyknischen Durchmischung im Ozean zum Beispiel entwickeln und implementieren wir neuartige Parametrisierungen, die energetisch konsistente Energiepfade von Oberflächen- und internen Wellen bis hin zu kleinräumigen Turbulenzen beschreiben. Hochauflösende ICON-O-Simulationen zeigen uns, wie wir verschiedene Energiereservoirs noch besser miteinander verbinden und die Performanz der Modelle weiter verbessern können.
Kreative experimentelle Konfigurationen
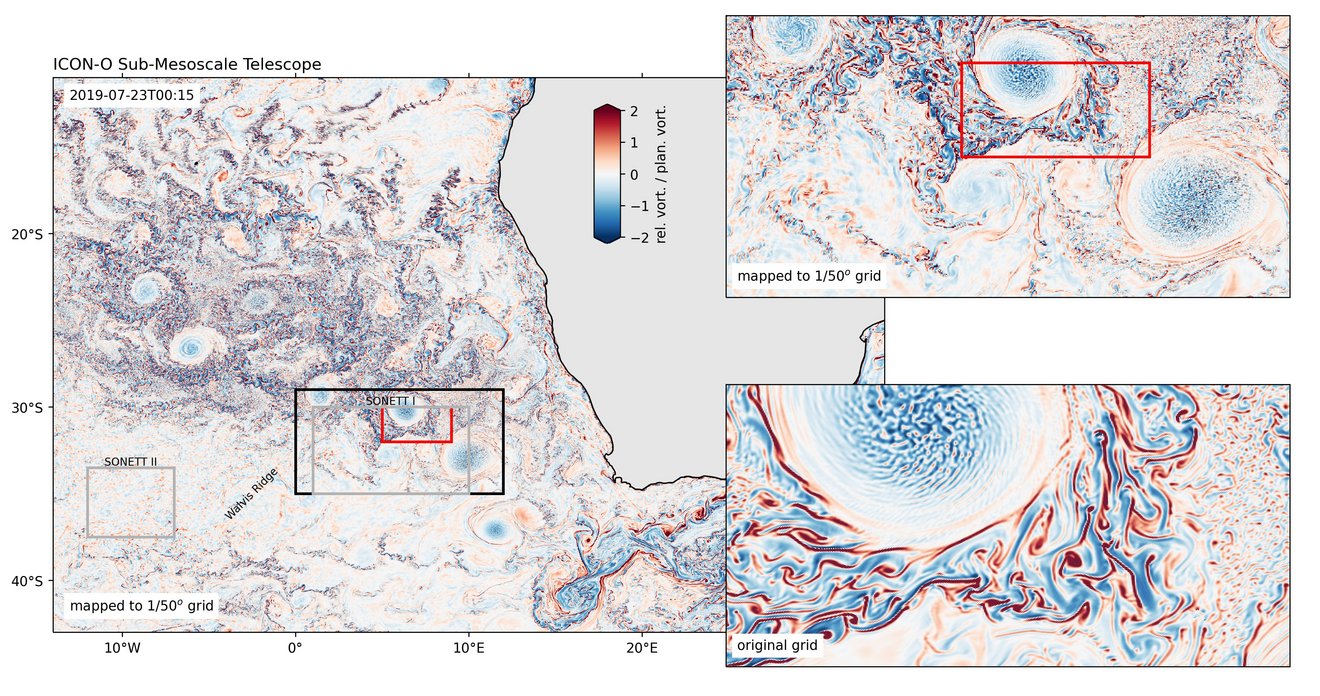
Um den Bereich der aufgelösten Skalen zu erweitern, stoßen wir mit hochauflösenden Simulationen in ozean-autonomen und gekoppelten Konfigurationen an die Grenzen der Rechenleistung. Ein Blick auf neue dynamische Regime, die jenseits der aktuell möglichen Auflösung globaler Ozeanmodelle liegen, kann durch die Verwendung einer *teleskopischen Modellkonfiguration* geworfen werden, die die Auflösung lokal erhöht und es erlaubt, z.B. submesoskalige Dynamik in einem realen Szenario zu untersuchen.
Neuartige Diagnostiken
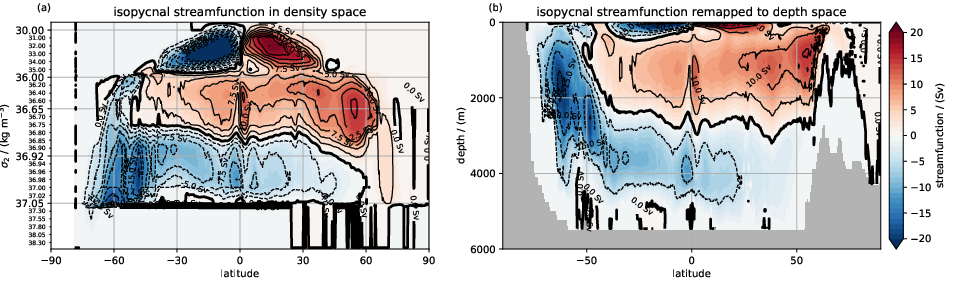
Die erhöhte räumliche Auflösung in vielen unserer Simulationen und die Konzentration auf kleinräumige Prozesse geht mit einer erheblichen Zunahme der zu analysierenden Daten einher. Wir untersuchen verschiedene ergänzende Ansätze, um solche Diagnosen auch für unsere größten Datensätze zu ermöglichen. In diesem Zusammenhang untersuchen wir eine verstärkte Nutzung von Online-Diagnosen, insbesondere für den Transport und den Energieaustausch.
Gruppenmitglieder und Publikationen
- Bastin, S., Koldunov, A., Schütte, F., Gutjahr, O., Mrozowska, M., Fischer, T., Shevchenko, R., Kumar, A., Koldunov, N., Haak, H., Brüggemann, N., Hummels, R., Specht, M., Jungclaus, J., Danilov, S., Dengler, M. & Jochum, M. (2025). Sensitivity of the tropical Atlantic to vertical mixing in two ocean models (ICON-O v2.6.6 and FESOM v2.5). Geoscientific Model Development, 18(4), 1189-1220. doi:10.5194/gmd-18-1189-2025 [publisher-version]
- Nielsen, D., Chegini, F., Serra, N., Kumar, A., Brüggemann, N., Hohenegger, C. & Ilyina, T. (2025). Resolved tropical cyclones trigger CO2 uptake and phytoplankton bloom in an Earth system model simulation. EarthArXiv, . doi:10.31223/X5KF05 [Preprint] [pre-print]
- Witte, M., Lapolli, F., Freese, P., Götschel, S., Ruprecht, D., Korn, P. & Kadow, C. (2025). Dynamic deep learning based super-resolution for the shallow water equations. Machine Learning: Science and Technology, 6: 015060. doi:10.1088/2632-2153/ada19f [publisher-version]
- Brüggemann, N., Losch, M., Scholz, P., Pollmann, F., Danilov, S., Gutjahr, O., Jungclaus, J., Koldunov, N., Korn, P., Olbers, D. & Eden, C. (2024). Parameterized internal wave mixing in three ocean general circulation models. Journal of Advances in Modeling Earth Systems, 16: e2023MS003768. doi:10.1029/2023MS003768 [research-data][publisher-version]
- Korn, P. & Titi, E. (2024). Global well-posedness of the primitive equations of large-scale ocean dynamics with the Gent-McWilliams-Redi Eddy Parametrization Model. SIAM journal on mathematical analysis, 56(6), 8011-8036. doi:10.1137/23M1564316 [publisher-version]
- Lapolli, F., da Silva Peixoto, P. & Korn, P. (2024). Accuracy and stability analysis of horizontal discretizations used in unstructured grid ocean models. Ocean Modelling, 189: 102335. doi:10.1016/j.ocemod.2024.102335 [publisher-version]
- Proske, U., Brüggemann, N., Gärtner, J., Gutjahr, O., Haak, H., Putrasahan, D. & Wieners, K.-H. (2024). A case for open communication of bugs in climate models, made with ICON version 2024.01. EGUsphere, . doi:10.5194/egusphere-2024-3493 [Preprint] [pre-print]
- Ssebandeke, J. (2024). Quantifying aspects of the ocean's energetics using eddy-resolving simulations. Phd Thesis, Berichte zur Erdsystemforschung, 279. [publisher-version]
- Ssebandeke, J., von Storch, J. & Brüggemann, N. (2024). Sensitivity of the global Lorenz energy cycle. Ocean Dynamics, available online.. doi:10.1007/s10236-023-01568-6 [publisher-version][supplementary-material]
- Crisan, D., Holm, D. & Korn, P. (2023). An implementation of Hasselmann’s paradigm for stochastic climate modelling based on stochastic Lie transport. Nonlinearity, 36, 4862-4903. doi:10.1088/1361-6544/ace1ce [publisher-version]
- Hohenegger, C., Korn, P., Linardakis, L., Redler, R., Schnur, R., Adamidis, P., Bao, J., Bastin, S., Behravesh, M., Bergemann, M., Biercamp, J., Bockelmann, H., Brokopf, R., Brüggemann, N., Casaroli, L., Chegini, F., Datseris, G., Esch, M., George, G., Giorgetta, M., Gutjahr, O., Haak, H., Hanke, M., Ilyina, T., Jahns, T., Jungclaus, J., Kern, M., Klocke, D., Kluft, L., Kölling, T., Kornblueh, L., Kosukhin, S., Kroll, C., Lee, J., Mauritsen, T., Mehlmann, C., Mieslinger, T., Naumann, A., Paccini, L., Peinado, A., Praturi, D., Putrasahan, D., Rast, S., Riddick, T., Roeber, N., Schmidt, H., Schulzweida, U., Schütte, F., Segura, H., Shevchenko, R., Singh, V., Specht, M., Stephan, C., von Storch, J., Vogel, R., Wengel, C., Winkler, M., Ziemen, F., Marotzke, J. & Stevens, B. (2023). ICON-Sapphire: simulating the components of the Earth System and their interactions at kilometer and subkilometer scales. Geoscientific Model Development, 16, 779-811. doi:10.5194/gmd-16-779-2023 [publisher-version]
- Sharma, K. & Korn, P. (2023). Numerical simulation of an idealized coupled ocean-atmosphere climate model. In Iske, A. & Rung, T. (Eds.), Modeling, Simulation and Optimization of Fluid Dynamic Applications (pp.113-130). Cham: Springer Nature . doi:10.1007/978-3-031-45158-4_7
- von Storch, J.-S., Hertwig, E., Lüschow, V., Brüggemann, N., Haak, H., Korn, P. & Singh, V. (2023). Open-ocean tides simulated by ICON-O. Geoscientific Model Development, 16, 5179-5196. doi:10.5194/gmd-16-5179-2023 [supplementary-material][publisher-version][any-fulltext]
- Danilov, S., Mehlmann, C. & Fofonova, V. (2022). On discretizing sea-ice dynamics on triangular meshes using vertex, cell or edge velocities. Ocean Modelling, 170: 101937. doi:10.1016/j.ocemod.2021.101937
- Jungclaus, J., Lorenz, S., Schmidt, H., Brovkin, V., Brüggemann, N., Chegini, F., Crueger, T., de Vrese, P., Gayler, V., Giorgetta, M., Gutjahr, O., Haak, H., Hagemann , S., Hanke, M., Ilyina, T., Korn, P., Kröger, J., Linardakis, L., Mehlmann, C., Mikolajewicz, U., Müller, W., Nabel, J., Notz, D., Pohlmann, H., Putrasahan, D., Raddatz, T., Ramme, L., Redler, R., Reick, C., Riddick, T., Sam, T., Schneck, R., Schnur, R., Schupfner, M., von Storch, J.-S., Wachsmann, F., Wieners, K.-H., Ziemen, F., Stevens, B., Marotzke, J. & Claussen, M. (2022). The ICON Earth System Model Version 1.0. Journal of Advances in Modeling Earth Systems, 14: e2021MS002813. doi:10.1029/2021MS002813 [publisher-version]
- Korn, P., Brüggemann, N., Jungclaus, J., Lorenz, S., Gutjahr, O., Haak, H., Linardakis, L., Mehlmann, C., Mikolajewicz, U., Notz, D., Putrasahan, D., Singh, V., von Storch, J.-S., Zhu , X. & Marotzke, J. (2022). ICON-O: The Ocean Component of the ICON Earth System Model - Global simulation characteristics and local telescoping capability. Journal of Advances in Modeling Earth Systems, 14: e2021MS002952. doi:10.1029/2021MS002952 [publisher-version]
- Kumar, A., Brüggemann, N., Smith, R. & Marotzke, J. (2022). Response of a tropical cyclone to a subsurface ocean eddy and the role of boundary layer dynamics. Quarterly Journal of the Royal Meteorological Society, 148, 378-402. doi:10.1002/qj.4210 [publisher-version]
- Linardakis, L., Stemmler, I., Hanke, M., Ramme, L., Chegini, F., Ilyina, T. & Korn, P. (2022). Improving scalability of Earth System Models through coarse-grained component concurrency - a case study with the ICON v2.6.5 modelling system. Geoscientific Model Development, 15, 9157-9176. doi:10.5194/gmd-15-9157-2022 [publisher-version]
- Mathis, M., Logemann, K., Maerz, J., Lacroix, F., Hagemann, S., Chegini, F., Ramme, L., Ilyina, T., Korn, P. & Schrum, C. (2022). Seamless integration of the coastal ocean in global marine carbon cycle modeling. Journal of Advances in Modeling Earth Systems, 14: e2021MS002789. doi:10.1029/2021MS002789 [publisher-version]
- Korn, P. (2021). Strong solvability of a variational data assimilation problem for the primitive equations of large-scale atmosphere and ocean dynamics. Journal of Nonlinear Science, 31: 56. doi:10.1007/s00332-021-09707-3 [publisher-version]
- Korn, P. (2021). Global well-posedness of the ocean primitive equations with nonlinear thermodynamics. Journal of Mathematical Fluid Mechanics, 23: 71. doi:10.1007/s00021-021-00596-w [publisher-version]
- Krönert, L. (2021). A split-explizit time-stepping scheme for ICON-Ocean. Phd Thesis, Hamburg: Universität Hamburg. Berichte zur Erdsystemforschung, 242. doi:10.17617/2.3311083 [publisher-version]
- Logemann, K., Linardakis, L., Korn, P. & Schrum, C. (2021). Global tide simulations with ICON-O: testing the model performance on highly irregular meshes. Ocean Dynamics, 71, 43-57. doi:10.1007/s10236-020-01428-7 [publisher-version]
- Mehlmann, C., Danilov, S., Losch, M., Lemieux, J., Hutter, N., Richter, T., Blain, P., Hunke, E. & Korn, P. (2021). Simulating linear kinematic features in viscous-plastic sea ice models on quadrilateral and triangular grids with different variable staggering. Journal of Advances in Modeling Earth Systems, 13: e2021MS002523. doi:10.1029/2021MS002523 [publisher-version]
- Mehlmann , C. & Richter, T. (2020). A goal oriented error estimator and mesh adaptivity for sea ice simulations. Ocean Modelling, 154: 101684. doi:10.1016/j.ocemod.2020.101684 [pre-print]
- Singh , V. & Frankel, S. (2020). On the use of split forms and wall modeling to enable accurate high-Reynolds number discontinuous Galerkin simulations on body-fitted unstructured grids. Computers & Fluids, 208: 104616. doi:10.1016/j.compfluid.2020.104616
- Korn, P. & Linardakis, L. (2018). A conservative discretization of the shallow-water equations on triangular grids. Journal of Computational Physics, 375, 871-900. doi:10.1016/j.jcp.2018.09.002
- Korn, P. (2018). A structure-preserving discretization of ocean parametrization on unstructured grids. Ocean Modelling, 132, 73-90. doi:10.1016/j.ocemod.2018.10.002
- Korn, P. (2018). A regularity-aware algorithm for variational data assimilation of an idealized coupled atmosphere–ocean model. Journal of Scientific Computing, 79, 748-786. doi:10.1007/s10915-018-0871-y [publisher-version]
- Ackmann, J. (2017). Error estimation algorithms for ocean models. Phd Thesis, Hamburg: Universität Hamburg. Berichte zur Erdsystemforschung, 186. doi:10.17617/2.2383652 [publisher-version]
- Ackmann, J., Marotzke, J. & Korn, P. (2017). Stochastic goal-oriented error estimation with memory. Journal of Computational Physics, 348, 195-219 . doi:10.1016/j.jcp.2017.07.009
- Korn, P. (2017). Formulation of an unstructured grid model for global ocean dynamics. Journal of Computational Physics, 339, 525-552. doi:10.1016/j.jcp.2017.03.009
- Korn, P. & Danilov, S. (2017). Elementary dispersion analysis of some mimetic discretizations on triangular C-grids. Journal of Computational Physics, 330, 156-172. doi:10.1016/j.jcp.2016.10.059
- Aizinger, V., Korn, P., Giorgetta, M. & Reich, S. (2015). Large-scale turbulence modelling via alpha-regularisation for atmospheric simulations. Journal of Turbulence, 16, 367-391. doi:10.1080/14685248.2014.991443
- Rauser, F., Marotzke, J. & Korn, P. (2015). Ensemble-type numerical uncertainty information from single model integrations. Journal of Computational Physics, 292, 30-42. doi:10.1016/j.jcp.2015.02.043
- Vlasenko, A., Korn, P., Riehme, J. & Naumann, U. (2014). Estimation of data assimilation error: A shallow-water model study. Monthly Weather Review, 142, 2502-2520. doi:10.1175/MWR-D-13-00205.1
- Korn, P. (2009). Data assimilation for the Navier-Stokes-alpha equations. Physica D: Nonlinear Phenomena, 238, 1957-1974. doi:10.1016/j.physd.2009.07.008
Kontakt
Dr. Nils Brüggemann
Gruppenleiter
Tel: +49 (0)40 41173-153
nils.brueggemann@mpimet.mpg.de
Dr. Peter Korn
Gruppenleiter
Tel: +49 (0)40 41173-470
peter.korn@mpimet.mpg.de
Weitere Themen
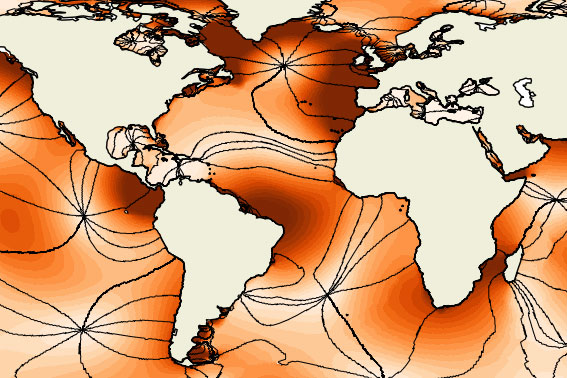
Auf dem Weg zur Auflösung der internen Gezeiten im Ozean
In einer kürzlich erschienenen Veröffentlichung zeigte Prof. Jin-Song von Storch zusammen mit anderen Wissenschaftler*innen, dass die Ozeankomponente…
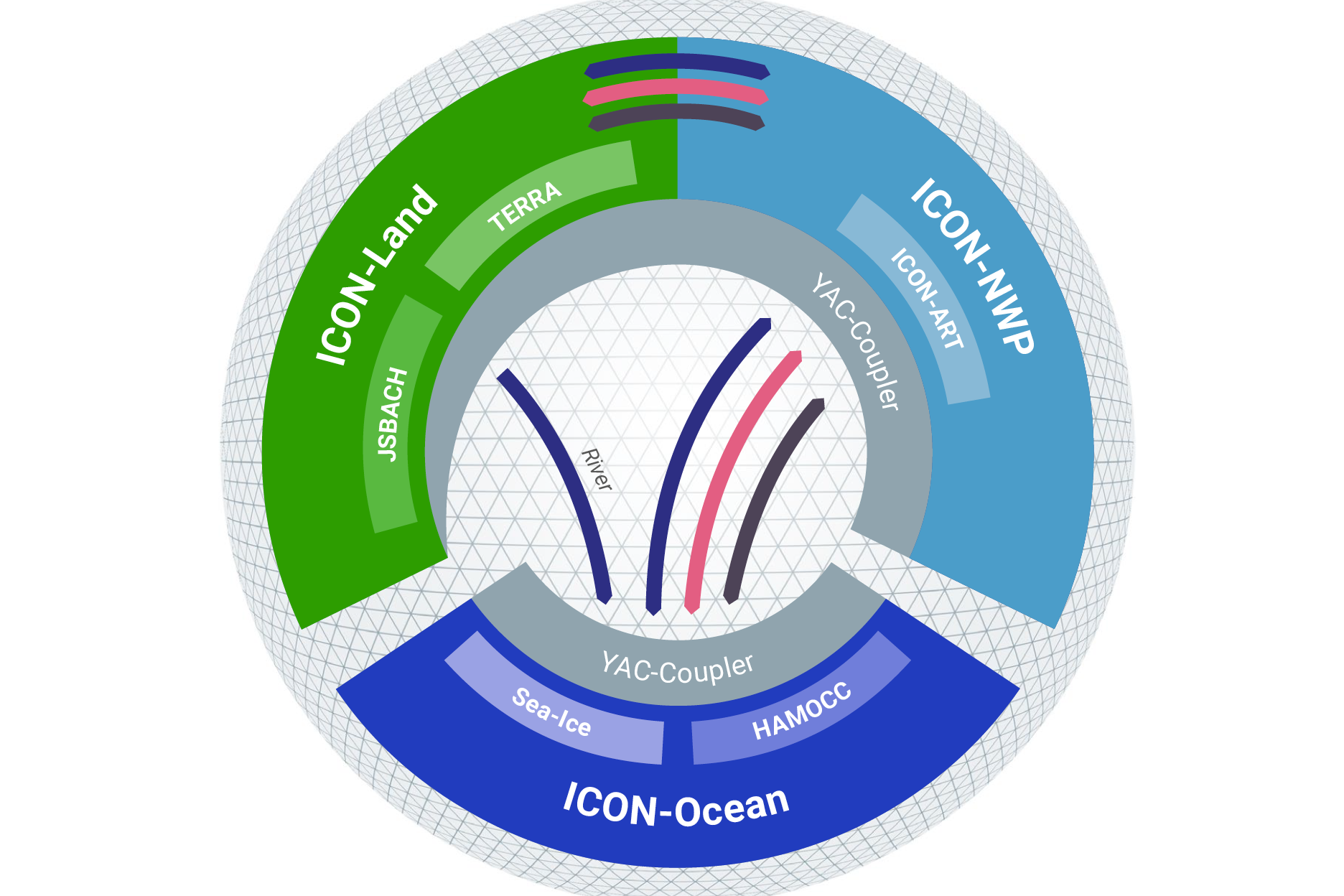
Wettervorhersage und Klimamodellierung rücken näher zusammen
Das Modell ICON lässt sich sowohl für die Wettervorhersage als auch für Klimavorhersagen und langfristige Projektionen nutzen. Bislang wurden die…

