Ozeanmodellierung am MPI-M – von LSG bis ICON-O

LSG – OPYC – HOPE – MPIOM
Autoren: Uwe Mikolajewicz und Peter Korn
Teil I - von Uwe Mikolajewicz
Zu Beginn der Forschung am MPI-M wurde der Ozean meist als Wärme speichernder und damit dämpfender Term in stochastischen Klimamodellen behandelt (Hasselmann, 1976). Aber der Wärmetransport des Ozeans ist ebenfalls wesentlich für das Klima. Daher schlug Klaus Hasselmann, Gründungsdirektor des MPI-M, vor, ein dreidimensionales Ozeanmodell für Klimastudien zu entwickeln, welches auch als Ozeankomponente in einem gekoppelten Atmosphäre-Ozean-Klimamodell genutzt werden sollte (Hasselmann, 1982).
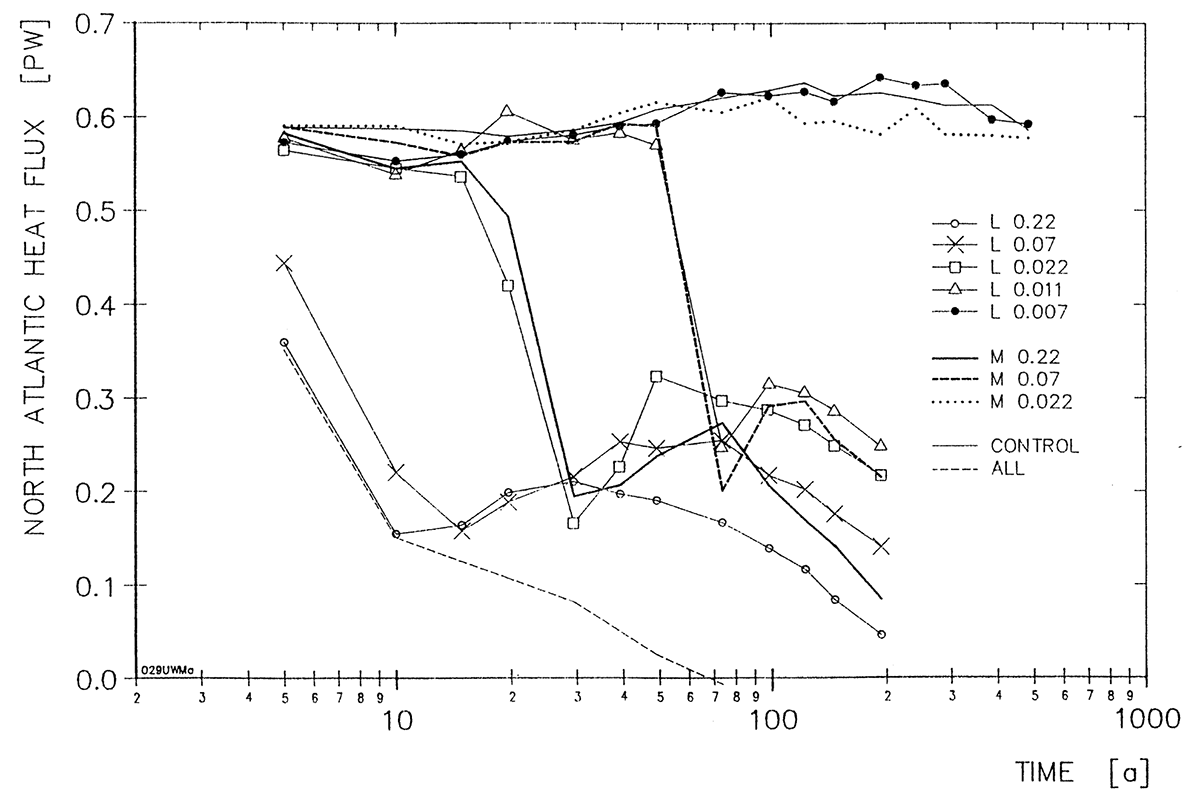
Basierend auf diesen Ideen entwickelte Ernst Maier-Reimer das großskalig-geostrophische Ozeanzirkulationsmodell (LSG) mit linearisierten Navier-Stokes-Gleichungen (Vernachlässigung der Impulsadvektion) und einem voll impliziten Zeitschrittalgorithmus (Maier-Reimer et al., 1982; Maier-Reimer et al., 1993). Bestimmende Terme für die Dynamik waren Geostrophie (die Balance zwischen Druckgradient und Coriolis-Kraft), Windantrieb und Reibung, was eine angemessene Näherung für den inneren Ozean darstellt (mit Ausnahme des Äquators). Mit einer horizontalen Auflösung von 5° war ein Zeitschritt von einem Monat möglich, was einen enormen Durchsatz von mehr als 500 Modelljahren pro Tag sogar auf den Computern der späten 1980er Jahre erlaubte. Das Modell hatte eine freie Oberfläche und beinhaltete ein einfaches thermodynamisches Meereismodell. Das LSG-Modell war sehr effizient für Langzeitintegrationen und erlaubte die Untersuchung des Effektes der Ozeanzirkulation auf das Klima. Das Modell wurde u.a. für verschiedene Paläo-Anwendungen genutzt. Ein Beispiel war die Überprüfung der Hypothese, dass die Kaltphase der Jüngeren Dryas vor 12.000 Jahren durch einen Süßwasserabfluss des zerfallenden Laurentinischen Eisschildes verursacht wurde. Maier-Reimer und Mikolajewicz (1989) zeigten, dass Süßwassereinträge in den Nordatlantik einen Zusammenbruch der atlantischen meridionalen Umwälzbewegung verursachen können, und dass die Sensitivität stark von dem Ort des Süßwassereintrags abhängt.
Das LSG-Modell war die Grundlage für das erste dreidimensionale anorganische Kohlenstoffkreislaufmodell (Maier-Reimer, 1984; Maier-Reimer und Hasselmann, 1987) und führte zur Entwicklung des Kohlenstoffkreislaufmodells des MPI-M HAMOCC (Bacastow und Maier-Reimer, 1990). Schon 1984 nutzte Maier-Reimer den Vorläufer von HAMOCC, um die Aufnahme des anthropogenen CO2 durch den Ozean abzuschätzen, und er hob hervor, wie wichtig die Tiefenwasserbildung in den hohen Breiten für die Aufnahme von überschüssigem CO2 ist (Maier-Reimer, 1984). Mit einem gekoppelten Ozean-Zirkulationsmodell mit marinem Kohlenstoffkreislauf konnten Maier-Reimer et al. (1996) die Effekte von nicht-konstantem Ozeanklima und Zirkulation auf die Kohlenstoffaufnahme in einer sich erwärmenden Welt untersuchen, welche die Fähigkeit des Ozeans zur Aufnahme von anthropogenem CO2 reduzieren.
Die Entwicklung eines adjungierten LSG-Modells machte die Inversmodellierung der stationären Ozeanzirkulation möglich. Damit kann ein Strömungsfeld erzeugt werden, das sowohl mit der Dynamik des Ozeanzirkulationsmodells als auch mit den Beobachtungen weitgehend konsistent war. Eine Anwendung war die Abschätzung der Ozeanzirkulation während des letzten glazialen Maximums, für das Proxy-Daten als Beobachtungsdaten verwendet wurden (Winguth et al., 1999).
Das LSG-Modell war die Ozeankomponente im ersten gekoppelten Atmosphäre-Ozean-Klimamodell des MPI-M (Cubasch et al., 1992), welches eines der ersten gekoppelten Klimamodelle war, mit dem die transienten Effekte zunehmender atmosphärischer CO2-Konzentrationen untersucht wurden. Diese Modellsimulationen zeigten schon die typischen Änderungen in der Ozeanzirkulation, die jetzt Standardergebnisse in Simulationen des anthropogenen Klimawandels sind, wie z.B. die Abschwächung der atlantischen Umwälzbewegung, die Abnahme des nach Norden gerichteten Wärmetransportes im Atlantik und ein Minimum der Erwärmung im nördlichen Nordatlantik.
Ein anderer Zweig in der Entwicklung der Ozeanzirkulationsmodelle am MPI-M war das isopyknische Ozeanmodell OPYC, welches Josef Oberhuber entwickelt hat (Oberhuber, 1993). In diesem Modell ist die vertikale Komponente nicht die Tiefe wie in anderen Ozeanmodellen des MPI-M, sondern die potentielle Dichte des Ozeans. Dieses Modell wurde auch als Ozeankomponente in einigen Versionen gekoppelter Klimamodelle des MPI-M benutzt (e.g., Roeckner et al., 1999).
Der Schwachpunkt der Approximationen im LSG-Modell ist die äquatoriale Dynamik. Deshalb entwickelte Ernst Maier-Reimer ein weiteres Ozeanmodell, welches auf einem vollständigeren Gleichungssatz, den primitiven Gleichungen, basierte. Das Modell hieß HOPE (Hamburg Ocean Primitive Equation model). Es wurde zunächst hauptsächlich auf den tropischen Pazifik angewendet, um die Dynamik von El Niño/Southern Oscillation (ENSO) zu untersuchen (Latif, 1987). Mit dem Modell konnten El Niño-Vorhersagen gemacht werden. Zunächst war es an ein einfaches empirisches Feedback-Modell gekoppelt, später an ein globales Zirkulationsmodell der Atmosphäre. Mittlerweile wurde das Modell zu einem globalen Modell erweitert, ein dynamisches/thermodynamisches Meereismodell wurde ergänzt und HOPE mit einem Atmosphärenmodell gekoppelt.
Die räumliche Diskretisierung von HOPE wurde in eine für hohe Auflösungen geeignetere geändert (von einem E-Gitter auf ein C-Gitter). Es wurde die Möglichkeit hinzugefügt, lokal orthogonale Gitter mit räumlich variierender Auflösung nutzen zu können (Maier-Reimer, 1997). Das erlaubte eine frei wählbare Platzierung der Gitterpole des Modells. Indem man die Gitterpole auf Land verlegte (z. B. Grönland), konnte die Singularität des Nordpols, ein Problem vieler globaler Ozeanmodelle zu der Zeit, leicht vermieden werden. So ein Modell-Setup erlaubt es, den Effekt des Meereistransports durch die Fram-Straße in den Nordatlantik mit einem globalen Modell zu untersuchen (Haak et al., 2003). In diesem globalen Setup wurden die Vorteile von regionaler hoher Auflösung und die Vermeidung von Problemen, die durch das Spezifizieren von Randbedingungen innerhalb des Ozeans auftreten, welches eines der Hauptprobleme regionaler Ozeanmodelle darstellt, kombiniert. Das Modell wurde später in MPIOM umbenannt und war in den letzten 15 Jahren die physikalische Ozeankomponente des MPI-Erdsystemmodells (Marsland et al., 2003; Jungclaus et al., 2013).
ICON: Seit den frühen 2000er Jahren
Teil II - von Peter Korn
Globale Ozeanmodelle streben mit Nachdruck eine optimale Recheneffizienz an und versuchen die Ressourcen des Hochleistungsrechnens maximal auszureizen. Recheneffizienz ist nicht nur eine „Nice-to-have“-Eigenschaft — sie ist ein „Must-have“, um die relevanten wissenschaftlichen Themen angehen zu können. Die Effizienzanforderungen zu erreichen, während zur gleichen Zeit die mathematischen Strukturen der beherrschenden partiellen Differentialgleichungen erfüllt werden müssen, stellt eine der Schlüsselherausforderungen in der numerischen Modellierung von geophysikalischen Flüssen dar.
Um die Jahrtausendwende wurde klar, dass die neuen Generationen der Supercomputer für die Klimamodellierung auf massiv paralleler Computerarchitektur beruhen würden. Zu dieser Zeit wurde die Ozeanklimamodellierung von strukturierten Gittermodellen dominiert: Ozeanmodelle auf Breitengrad-Längengrad-Gittern. Die Parkettierung der Kugelfläche mit rechteckigen orthogonalen Gittern verursacht eine starke Ungleichmäßigkeit in der Gitterauflösung – die Pol-Singularität – und diese Ungleichmäßigkeit begrenzt die Recheneffizienz auf massiv parallelen Rechnerplattformen. Daher leiden die Modelle mit strukturierten Gittern unter einem Dilemma zwischen dem Bedarf an Hochleistungsrechnen und den Fakten der Kugelgeometrie: sie müssen entweder rechteckig oder gleichmäßig sein.
Der Weg aus diesem Dilemma sind unstrukturierte Gitter, Gitter mit nicht-rechteckigen Zellengeometrien. Unter den vielfältigen vorstellbaren unstrukturierten Gittern hat eine spezielle Klasse die größte Aufmerksamkeit erregt, ein Satz von Gittern, der aus höchst regelmäßigen geometrischen Objekten hervorgeht – den platonischen Körpern. Das MPI-M hat einen bestimmten platonischen Körper als Grundlage für seine neue Modellgeneration ausgewählt – das Ikosaeder.
Das ICON-Projekt stellt die Rahmenbedingungen bereit, in denen das MPI-M seine Tradition der Ozeanmodellentwicklung fortsetzt und seine Modellierungsstrategie an die neu aufkommenden Technologien im Hochleistungsrechnen anpasst. Die Nutzung des neuen ikosaedrischen Gitters zwingt uns, die fundamentalen physikalischen Gesetze der Ozeandynamik, die unseren Modellen zu Grunde liegen, zu überdenken und sie sinnvoller für Computercodes umzuschreiben, die effizient auf massiv parallelen Computerarchitekturen laufen.
Während des Verlaufs des ICON-Projekts stellte sich heraus, dass alle unstrukturierten Gitter einen gemeinsamen Nachteil haben: unabhängig davon, wie man die Modellvariablen auf dem Gitter verteilt, generiert man immer unechte Wellen oder Rechenmoden, die keine physikalische Bedeutung haben und die Lösung verunreinigen.
Die Wahl des MPI-M, eine variable Staffelung („staggering“) auf dem ikosaedrischen Gitter vorzunehmen, ist attraktiv. Sie ist aber besonders schwierig, wenn nicht sogar unmöglich zu nutzen, da es zu Rechenmoden in der Kontinuitätsgleichung des Modells führt, für die es keine rechnerische Auflösung gab. Daher haben verschiedene Modelliergruppen dieses Gitter aufgegeben und andere Gitter und variable Aufteilungen gewählt. Die Lösung für das Problem am MPI-M kam aus der Mathematik.
Für die umfassende Ausführung des allgemeinen Ozeanzirkulationsmodells ICON-O ist die Kontrolle über die unechten Moden nur ein Aspekt der erwünschten Modelleigenschaften. Erhaltungseigenschaften sind von größter Wichtigkeit für die Langzeitrechnungen in der Ozeanmodellierung. Das Design von ICON-O basiert auf den eigenständigen Erhaltungssätzen. Mathematisch sind die Erhaltungssätze eng mit der Variationsform der beherrschenden Gleichungen in geeigneten Hilbert-Räumen verbunden. Die beiden wesentlichen Hemmnisse beim Implementieren der Erhaltungssätze sind die Handhabung der einzelnen Differentialoperatoren und der Rekonstruktionen, die durch die variable Staffelung zur Berechnung von Flüssen benötigt werden. Es stellte sich heraus, dass die mathematische Vereinbarkeit der differentiellen Operatoren und der Rekonstruktionen mit der diskreten Variationsform der primitiven Gleichungen für den Ozean der Schlüssel ist. Er garantiert die Erhaltungssätze und integriert gleichzeitig auf natürliche Weise einen zur Physik kompatiblen Filter, welcher die unechten Moden kontrolliert (Korn, 2017; Korn und Danilov, 2017).
Die Analyse der Ergebniszahlen offenbart zusätzliche positive Überraschungen. Sie führt zu einer natürlichen und neuen Diskretisierung einer wesentlichen ozeanischen kleinskaligen Parametrisierung unterhalb der Gitterauflösung. Die „isoneutrale Diffusion“ und die „Wirbel-Parametrisierung“ von Gent-McWilliams sind Meilensteine in der Ozeanmodellierung und werden nahezu in jedem Ozeanzirkulationsmodell verwendet. Die Berechnung dieser Parametrisierungen wirft ein tiefgehendes Diskretisierungsproblem auf, für das seit den späten 1990er Jahren nur eine Lösung bekannt war. Die numerischen Mechanismen von ICON-O präsentieren eine neue Lösung für dieses Problem, indem inhärent unstrukturierte Gittermethoden verwendet werden (Korn, 2018). Eine zweite Überraschung ergab sich aus der Anwendung der Diskretisierung von ICON-O auf die Flachwassergleichungen. Die Flachwassergleichungen sind ein vereinfachter Satz von Gleichungen in der geophysikalischen Strömungsdynamik, die nichtsdestotrotz einige der wesentlichen Aspekte der atmosphärischen oder ozeanischen Zirkulation beinhalten. Das Bemerkenswerte an ICON-O ist, dass es sowohl die Gesamtenergie als auch die potentielle Enstrophie erhält (Korn and Linardakis, 2018). Die meisten anderen Modelle erhalten nur eines von beiden. Beide quadratischen Erhaltungsgrößen numerisch zu erhalten, stellt eine ähnlich große Errungenschaft dar wie die bedeutende Arakawa-Diskretisierung von 1990.
Nach der Entwicklung einer fundamentalen neuer Numerik und ihrer Analyse können wir jetzt ICON-O zum „Arbeitspferd“ des MPI-M für Simulationen mit hoher Auflösung in gekoppelten und in eigenständigen Konfigurationen machen.
Literatur Teil I
Bacastow, R. and E. Maier-Reimer (1990) Ocean-circulation of the carbon cycle. Climate Dyn., 4, 95-125.
Cubasch, U., Hasselmann, K., Höck, H., Maier-Reimer, E., Mikolajewicz, U., Santer, B. D. and R. Sausen (1992) Time-dependent greenhouse warming computations with a coupled ocean-atmosphere model. Climate Dynamics, 8, 55-69.
Haak, H., Jungclaus, J., Mikolajewicz, U. and M. Latif (2003) Formation and propagation of great salinity anomalies. Geophysical Research Letters, 30, Art. No. 1473, doi: 10.1029/2003GL017065.
Hasselmann, K. (1976) Stochastic climate models, Part I, Theory. Tellus, 28, 473.
Hasselmann, K. (1982) An ocean model for climate variability studies. Progr. Oceanogr., 11, 69-92.
Jungclaus, J.H., Fischer, N., Haak, H., Lohmann, K., Marotzke, J., Matei, D., Mikolajewicz, U., Notz, D. and J.-S. von Storch (2013). Characteristics of the ocean simulations in MPIOM, the ocean component of the MPI-Earth System Model. J. Adv. Model. Earth. Syst. 5, 422-446. doi:10.1002/jame.20023.
Latif, M. (1987) Tropical Ocean Circulation Experiments. J. Phys. Oc., 17 (2), 246-263.
Maier-Reimer, E., Müller, D., Olbers, D., Willebrand, J., & Hasselmann, K. F. (1982) An ocean circulation model for climate variability studies. Hamburg: Max-Planck-Institut für Meteorologie. (Umweltforschungsplan des Bundesministers des Innern - Entwicklung von Klimamodellen; FB 104 02 612)
Maier-Reimer E. (1984) Towards a global ocean carbon model. Progress in Biometeorology, 3, 295–310.
Maier-Reimer, E. and K. Hasselmann (1987) Transport and storage of CO2 in the ocean – an inorganic ocean-circulation carbon cycle model. Climate Dynamics, 2, 63; https://doi.org/10.1007/BF01054491.
Maier-Reimer, E. and U. Mikolajewicz (1989) Experiments with an OGCM on the cause of the Younger Dryas. In A. Ayala-Castanares, W. Wooster and A. Yañez-Aranciba (eds.), Oceanography 1988. p. 87 - 100, UNAM Press, Mexico D.F. 207p.
Maier-Reimer, E., Mikolajewicz, U. and K. Hasselmann (1993) Mean circulation of the Hamburg LSG OGCM and its sensitivity to the thermohaline surface forcing. Journal of Physical Oceanography, 23, 731-757.
Maier-Reimer, E., U. Mikolajewicz and A. Winguth (1996) Interactions between ocean circulation and the biological pumps in the global warming. Climate Dynamics, 12, 711-721.
Maier-Reimer, E. (1997) Design of a closed boundary regional model of the Arctic Ocean. /Workshop on Polar Processes in Global Climate/ (pp. 72-73). Boston: American Meteorological Society
Marsland, S.J., Haak, H., Jungclaus, J.H. and M. Latif (2003) The Max Planck Institute global ocean/sea ice model with orthogonal curvilinear coordinates. Ocean Modelling, 5 (2), 91-127; doi: 10.1016/S1463-5003(02)00015-X
Mikolajewicz, U., and E. Maier-Reimer (1994) Mixed boundary conditions in ocean general circulation models and their influence on the stability of the model’s conveyor belt. Journal of Geophysical Research, 99, C11, 22,633-22,644.
Oberhuber, J.M. (1993) Simulation of the Atlantic circulation with a coupled sea ice - mixed layer - isopycnal General Circulation Model. Part I: Model Description. J. Phys. Oceanogr., 23, 808-829.
Roeckner, E., Bengtsson, L., Feichter, J., Lelieveld, J. and H. Rohde (1999) Transient climate change simulations with a coupled atmosphere-ocean GCM including the tropospheric sulfur cycle. J. Climate, 12, 2004-3032.
Winguth, A. M. E., Archer, D., Maier-Reimer, E., Mikolajewicz, U. and J.-C. Duplessy (1999). Sensitivity of paleo nutrient tracer distributions and deep-sea circulation to glacial conditions. Paleoceanography, 14, 304-323.
Literatur Teil II
Korn, P. (2017) Formulation of an unstructured grid model for global ocean dynamics. J. of Comp. Phys., 339, 525-552. doi.org/10.1016/j.jcp.2017.03.009
Korn, P. and S. Danilov (2017) Elementary dispersion analysis of some mimetic discretizations on triangular C-grid. J. of Comp. Phys., 330, 156-172. doi.org/10.1016/j.jcp.2016.10.059
Korn, P. (2018) A structure preserving discretization of ocean parametrizations on unstructured grids. Ocean Modelling, 132, 73-90. doi.org/10.1016/j.ocemod.2018.10.002
Korn, P. and L. Linardakis (2018) A conservative discretization of the shallow-water equations on triangular grid. J. of Comp. Phys., 375, 871-900. doi.org/10.1016/j.jcp.2018.09.002
Kontakt
Uwe Mikolajewicz
Max-Planck-Institut für Meteorologie
Tel.: 040 41173 243
E-Mail: uwe.mikolajewicz@mpimet.mpg.de
Dr. Peter Korn
Max-Planck-Institut für Meteorologie
Tel.: 040 41173 470
E-Mail: peter.korn@mpimet.mpg.de
