Ocean modelling at MPI-M – from LSG to ICON-O
LSG – OPYC – HOPE – MPIOM
Authors: Uwe Mikolajewicz and Peter Korn
Part I - by Uwe Mikolajewicz
In the beginning of the research at MPI-M, the ocean was mostly considered as a damping and storage term in the stochastic climate models (Hasselmann, 1976). But ocean heat transport is also essential for climate. Therefore, Klaus Hasselmann, founding director of the MPI-M, suggested the outline of a 3-dimensional ocean model designed for climate studies, which could also act as the ocean component in a coupled atmosphere-ocean climate model (Hasselmann, 1982).
Based on these ideas, Ernst Maier-Reimer developed the Large-Scale-Geostrophic ocean general circulation model (LSG) using linearized Navier-Stokes equations (neglecting advection of momentum) and a fully implicit time-stepping algorithm (Maier-Reimer et al., 1982; Maier-Reimer et al., 1993). The dominant terms for the dynamics were geostrophy (the balance between pressure gradients and Coriolis force), wind forcing and friction, which is an appropriate approximation for the interior of the ocean (except at the equator). With a horizontal resolution of 5°, a time step of 1 month was achievable, allowing a tremendous turnaround of more than 500 model years/day even on the computers available in the late 1980s. The model had a free surface and a simple thermodynamic sea ice model. The LSG model was very efficient for long-term integrations and allowed the investigation of the ocean effect on climate. The model has also been applied to several paleo applications. One example was to test the hypothesis that the Younger Dryas cold event about 12,000 years ago was caused by freshwater input from the decaying Laurentide ice sheet. Maier-Reimer and Mikolajewicz (1989) showed that freshwater input into the North Atlantic can cause a breakdown of the Atlantic’s meridional overturning circulation and that the sensitivity depends strongly on the location of the freshwater input (see Fig.).
The LSG model provided the basis for the first three-dimensional inorganic carbon cycle model (Maier-Reimer, 1984; Maier-Reimer and Hasselmann, 1987) and allowed the development of MPI-M’s carbon cycle model HAMOCC (Bacastow and Maier-Reimer, 1990). Already in 1984, Maier-Reimer used the precursor of HAMOCC to estimate the ocean uptake of anthropogenic CO2 and emphasized the important role of high-latitude deep-water formation on the uptake of excess CO2 (Maier-Reimer, 1984). With a coupled ocean general circulation-marine carbon cycle model, Maier-Reimer et al. (1996) pioneered investigating the effects of non-constant ocean climate and circulation on carbon uptake in a warming world, which reduce the ability of the ocean to take up anthropogenic CO2.
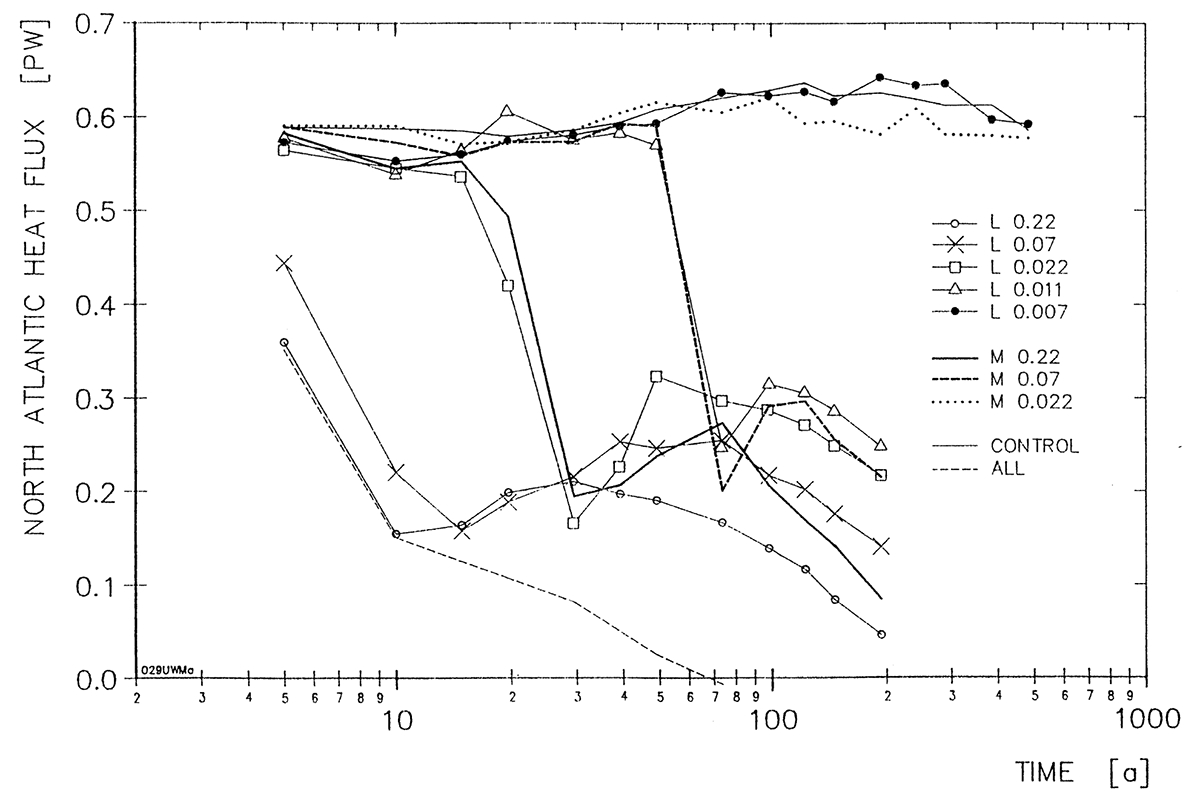
The development of an adjoint of the LSG model allowed steady-state inverse estimates of the ocean circulation that are consistent with both the dynamics of an ocean GCM and observational data. One application was the estimate of the ocean circulation of the Last Glacial Maximum using proxy data as observational constraint (Winguth et al., 1999).
The LSG model served as the ocean component in the first MPI-M coupled atmosphere-ocean climate model (Cubasch et al., 1992), which was one of the first coupled climate models applied to study the transient effect of rising atmospheric CO2 concentrations. These model simulations already showed the typical changes in ocean circulation that are now standard results in anthropogenic climate change, such as a weakening of the Atlantic overturning circulation, reduction of the northward heat transport of the Atlantic, and a minimum of the warming in the northern North Atlantic.
Another branch of ocean model development at MPI-M was the isopycnic ocean model OPYC developed by Josef Oberhuber (Oberhuber, 1993). Here the vertical coordinate was not the depth as in the other ocean models at MPI-M, but ocean potential density. This model served also as ocean component in some versions of the coupled climate model at MPI-M (e.g., Roeckner et al., 1999).
The weak point of the approximations used in the LSG model is the equatorial dynamics. Therefore Ernst Maier-Reimer developed another ocean model based on a more complete set of equations, named primitive equations. The model was called HOPE model (Hamburg Ocean Primitive Equation model). It was at first primarily applied to the tropical Pacific studying the dynamics of El Niño/Southern Oscillation (ENSO) (Latif, 1987). Coupled at first to a simple empirical feedback model and later to an atmospheric GCM, it allowed predictions of El Niño. During time, the model was extended into a global model, a dynamic/thermodynamic sea ice model was added, and HOPE was coupled to an atmosphere model.
The spatial discretization of HOPE was changed into one more suitable for high resolutions (from an E-grid to a C-grid). The option to use locally orthogonal grids with spatially varying resolution was added (Maier-Reimer, 1997). This allowed an arbitrary placement of the model’s grid poles. Thus, the singularity at the North Pole, a problem of many global ocean models at that time, could easily be avoided by placing the grid poles on land (e.g., Greenland). Such a model setup allowed studying the effect of Fram Strait sea ice export on the North Atlantic using a global model (Haak et al., 2003), thus combining the advantages of regionally high resolution and avoiding problems with having to specify boundary conditions inside the ocean, one main problem of regional ocean models. This model has later been renamed MPIOM and has been the physical ocean component of the MPI Earth System Model for the last 15 years (Marsland et al., 2003; Jungclaus et al., 2013).
ICON: Since the early 2000s
Part II (by Peter Korn)
Global ocean models strive forcefully for optimal computational efficiency and try to explore the resources of the high-performance computing environment to a maximum degree. Computational efficiency is not only a “nice-to-have”-property – it is a “must-have” in order to tackle the relevant scientific problems. To satisfy efficiency demands while at the same time comply with the mathematical structure of the governing partial differential equations (PDE’s) constitutes one of the key challenges in numerical modelling of geophysical flows.
Around the turn of the millennium it became evident that the forthcoming generations of supercomputers used in climate modelling will rely on massively parallel computing architectures. At this time the field of ocean climate modelling was dominated by “structured-grid models” –ocean models on latitude-longitude grids. The tessellation of the sphere with rectangular orthogonal grids causes a strong non-uniformity in the resolution of the grid – the polar singularity – and this non-uniformity limits the computational efficiency on massively parallel computing platforms. Thus, structured-grid ocean models suffer from a dilemma between the needs of high-performance computing and the facts of spherical geometry: either being rectangular or being uniform.
The way out of this dilemma is to consider unstructured grids, grids with non-rectangular cell geometries. Among the manifold of imaginable unstructured grids, a specific class has attracted the greatest attention, a set of grids that emanate from highly regular geometric objects – the Platonic solids. MPI-M has chosen one particular Platonic solid as foundation of its new model generation – the Icosahedron.
The ICON project provides the framework in which MPI-M continues its tradition of ocean model development and adapts its modelling strategy to new emerging technologies in high-performance computing. The use of the new icosahedral grid compels us to revisit the fundamental physical laws of ocean dynamics underlying our models and to transform them sensibly to computer codes that are capable of running efficiently on massively parallel computing architectures.
During the progression of the ICON project it was discovered that all unstructured grids share a common disadvantage: regardless how one distributes the model variables on the grid, one always generates spurious waves or computational modes that have no physical meaning and contaminate the solution.
MPI-M’s choice of variable staggering on the icosahedral grid was considered attractive but particular difficult if not impossible to use since it suffers from a computational mode in the model’s continuity equations for which no computational cure was known. Therefore, several modelling groups have abandoned this grid and chosen different grids and variable layouts. The solution to MPI-M’s problem came from mathematics.
For the overall design of the ocean general circulation model ICON-O, the control of spurious modes is just one aspect of desirable model properties. Conservation properties are of paramount importance for the longtime integrations required in ocean modelling. The design of ICON-O is centered on discrete conservation principles. Mathematically, conservation principles are intimately linked with the variational form of the governing equations in appropriate Hilbert spaces. The two key building blocks in implementing conservation principles are the treatment of discrete differential operators and of the reconstructions that are required by the variable staggering in order to calculate fluxes. It turned out that imposing the mathematical compatibility of both differential operators and reconstructions with the discrete variational form of the ocean primitive equations is the key that guarantees conservation principles and at the same time integrates in a natural way a physics-compatible filter that controls the spurious mode (Korn, 2017; Korn and Danilov, 2017).
The analysis of the resulting numerics revealed additional positive surprises. It leads to a natural and new discretization of an essential oceanic sub-grid scale parametrization. The “isoneutral diffusion” and the “eddy parametrization” of Gent-McWilliams are milestones in ocean modelling and are applied by virtually every ocean general circulation model. The actual computation of these parametrizations poses a subtle discretization problem for which since the late 1990’s only one solution was known. Using ICON-O’s numerical machinery provided a new solution to this problem that employs inherently unstructured methods (Korn, 2018). A second surprise was provided by the application of the ICON-O discretization to the shallow water equations. These equations are a simplified set of equations of geophysical fluid dynamics that nevertheless contain some of the key aspects of the atmospheric or oceanic circulation. The remarkable property of the ICON-O numerics is that it preserves both quadratic invariants, total energy and potential enstrophy (Korn and Linardakis, 2018). Most other schemes preserve only one of them. The conservation of both quadratic invariants puts the numerical scheme in the same category as the famous Arakawa discretization from 1990.
After inventing fundamentally new numerics and analyzing these numerics we can now turn ICON-O into MPI-M’s workhorse for high-resolution simulations in coupled as well as in stand-alone configurations.
References Part I
Bacastow, R. and E. Maier-Reimer (1990) Ocean-circulation of the carbon cycle. Climate Dyn., 4, 95-125.
Cubasch, U., Hasselmann, K., Höck, H., Maier-Reimer, E., Mikolajewicz, U., Santer, B. D. and R. Sausen (1992) Time-dependent greenhouse warming computations with a coupled ocean-atmosphere model. Climate Dynamics, 8, 55-69.
Haak, H., Jungclaus, J., Mikolajewicz, U. and M. Latif (2003) Formation and propagation of great salinity anomalies. Geophysical Research Letters, 30, Art. No. 1473, doi: 10.1029/2003GL017065.
Hasselmann, K. (1976) Stochastic climate models, Part I, Theory. Tellus, 28, 473.
Hasselmann, K. (1982) An ocean model for climate variability studies. Progr. Oceanogr., 11, 69-92.
Jungclaus, J.H., Fischer, N., Haak, H., Lohmann, K., Marotzke, J., Matei, D., Mikolajewicz, U., Notz, D. and J.-S. von Storch (2013). Characteristics of the ocean simulations in MPIOM, the ocean component of the MPI-Earth System Model. J. Adv. Model. Earth. Syst. 5, 422-446. doi:10.1002/jame.20023.
Latif, M. (1987) Tropical Ocean Circulation Experiments. J. Phys. Oc., 17 (2), 246-263.
Maier-Reimer, E., Müller, D., Olbers, D., Willebrand, J., & Hasselmann, K. F. (1982) An ocean circulation model for climate variability studies. Hamburg: Max-Planck-Institut für Meteorologie. (Umweltforschungsplan des Bundesministers des Innern - Entwicklung von Klimamodellen; FB 104 02 612)
Maier-Reimer E. (1984) Towards a global ocean carbon model. Progress in Biometeorology, 3, 295–310.
Maier-Reimer, E. and K. Hasselmann (1987) Transport and storage of CO2 in the ocean – an inorganic ocean-circulation carbon cycle model. Climate Dynamics, 2, 63; https://doi.org/10.1007/BF01054491.
Maier-Reimer, E. and U. Mikolajewicz (1989) Experiments with an OGCM on the cause of the Younger Dryas. In A. Ayala-Castanares, W. Wooster and A. Yañez-Aranciba (eds.), Oceanography 1988. p. 87 - 100, UNAM Press, Mexico D.F. 207p.
Maier-Reimer, E., Mikolajewicz, U. and K. Hasselmann (1993) Mean circulation of the Hamburg LSG OGCM and its sensitivity to the thermohaline surface forcing. Journal of Physical Oceanography, 23, 731-757.
Maier-Reimer, E., U. Mikolajewicz and A. Winguth (1996) Interactions between ocean circulation and the biological pumps in the global warming. Climate Dynamics, 12, 711-721.
Maier-Reimer, E. (1997) Design of a closed boundary regional model of the Arctic Ocean. /Workshop on Polar Processes in Global Climate/ (pp. 72-73). Boston: American Meteorological Society
Marsland, S.J., Haak, H., Jungclaus, J.H. and M. Latif (2003) The Max Planck Institute global ocean/sea ice model with orthogonal curvilinear coordinates. Ocean Modelling, 5 (2), 91-127; doi: 10.1016/S1463-5003(02)00015-X
Mikolajewicz, U., and E. Maier-Reimer (1994) Mixed boundary conditions in ocean general circulation models and their influence on the stability of the model’s conveyor belt. Journal of Geophysical Research, 99, C11, 22,633-22,644.
Oberhuber, J.M. (1993) Simulation of the Atlantic circulation with a coupled sea ice - mixed layer - isopycnal General Circulation Model. Part I: Model Description. J. Phys. Oceanogr., 23, 808-829.
Roeckner, E., Bengtsson, L., Feichter, J., Lelieveld, J. and H. Rohde (1999) Transient climate change simulations with a coupled atmosphere-ocean GCM including the tropospheric sulfur cycle. J. Climate, 12, 2004-3032.
Winguth, A. M. E., Archer, D., Maier-Reimer, E., Mikolajewicz, U. and J.-C. Duplessy (1999). Sensitivity of paleo nutrient tracer distributions and deep-sea circulation to glacial conditions. Paleoceanography, 14, 304-323.
References Part II
Korn, P. (2017) Formulation of an unstructured grid model for global ocean dynamics. J. of Comp. Phys., 339, 525-552. doi.org/10.1016/j.jcp.2017.03.009
Korn, P. and S. Danilov (2017) Elementary dispersion analysis of some mimetic discretizations on triangular C-grid. J. of Comp. Phys., 330, 156-172. doi.org/10.1016/j.jcp.2016.10.059
Korn, P. (2018) A structure preserving discretization of ocean parametrizations on unstructured grids. Ocean Modelling, 132, 73-90. doi.org/10.1016/j.ocemod.2018.10.002
Korn, P. and L. Linardakis (2018) A conservative discretization of the shallow-water equations on triangular grid. J. of Comp. Phys., 375, 871-900. doi.org/10.1016/j.jcp.2018.09.002
Contact
Uwe Mikolajewicz
Max Planck Institute for Meteorology
Phone: +49 (0) 40 41173 243
Email: uwe.mikolajewicz@mpimet.mpg.de
Dr. Peter Korn
Max Planck Institute for Meteorology
Phone: +49 (0) 40 41173 470
Email: peter.korn@mpimet.mpg.de

