Ist das Klima deterministisch oder stochastisch?
Die zeitliche Entwicklung des Klimas wird durch Gleichungen beschrieben, in denen die zeitliche Ableitung einer Klimavariablen x gleich der verantwortlichen Dynamik f ist und somit folgende Bedingungen erfüllt dx / dt = f . Der Zeitableitungsoperator ist ein Hochpassfilter. Dies hat schwerwiegende Folgen für die interne Klimavariabilität auf ultralangen Zeitskalen. Entgegen dem allgemeinen Verständnis zeigt Prof. von Storch, dass diese langzeitliche Variabilität nicht mit der dafür verantwortlichen internen Dynamik auf denselben Zeitskalen entschlüsselt werden kann.
Die Autorin zieht ihre Schlussfolgerung für ein Gleichgewichtsklima, das unter einem konstanten äußeren Antrieb erreicht wird. Grundlage hierfür ist eine sorgfältige Zerlegung der gesamten Gleichgewichtsvarianz in Form von Spektren, unterstützt durch die Spektren, die aus dem Lorenz-Modell (Lorenz, 1963) als vereinfachtem Klimamodell abgeleitet werden. Einerseits unterdrückt der Zeitableitungsoperator Variationen der internen Dynamik auf ultralangen Zeitskalen, was mit der Tatsache vereinbar ist, dass die interne Dynamik nur auf endlichen Zeitskalen funktioniert (da sonst kein Gleichgewichtszustand erreicht werden kann). Andererseits variiert eine Gleichgewichtsklimalösung auf allen Zeitskalen, einschließlich der unendlichen Zeitskalen, da die Gleichgewichtslösung – wenn sie mit demselben konstanten externen Antrieb allein gelassen wird – bis in unendliche Zeiten hinein stationär variiert. Somit ist das Spektrum einer Klimavariablen x auf fast-unendlichen und unendlichen Zeitskalen weiß und nicht null, während das Spektrum des verantwortlichen dynamischen Antriebs f auf fast-unendlichen Zeitskalen de facto null ist und auf unendlichen Zeitskalen genau null, was zu einem Zusammenbruch der Kohärenz zwischen x und f auf ultralangen Zeitskalen führt (siehe Abbildung).
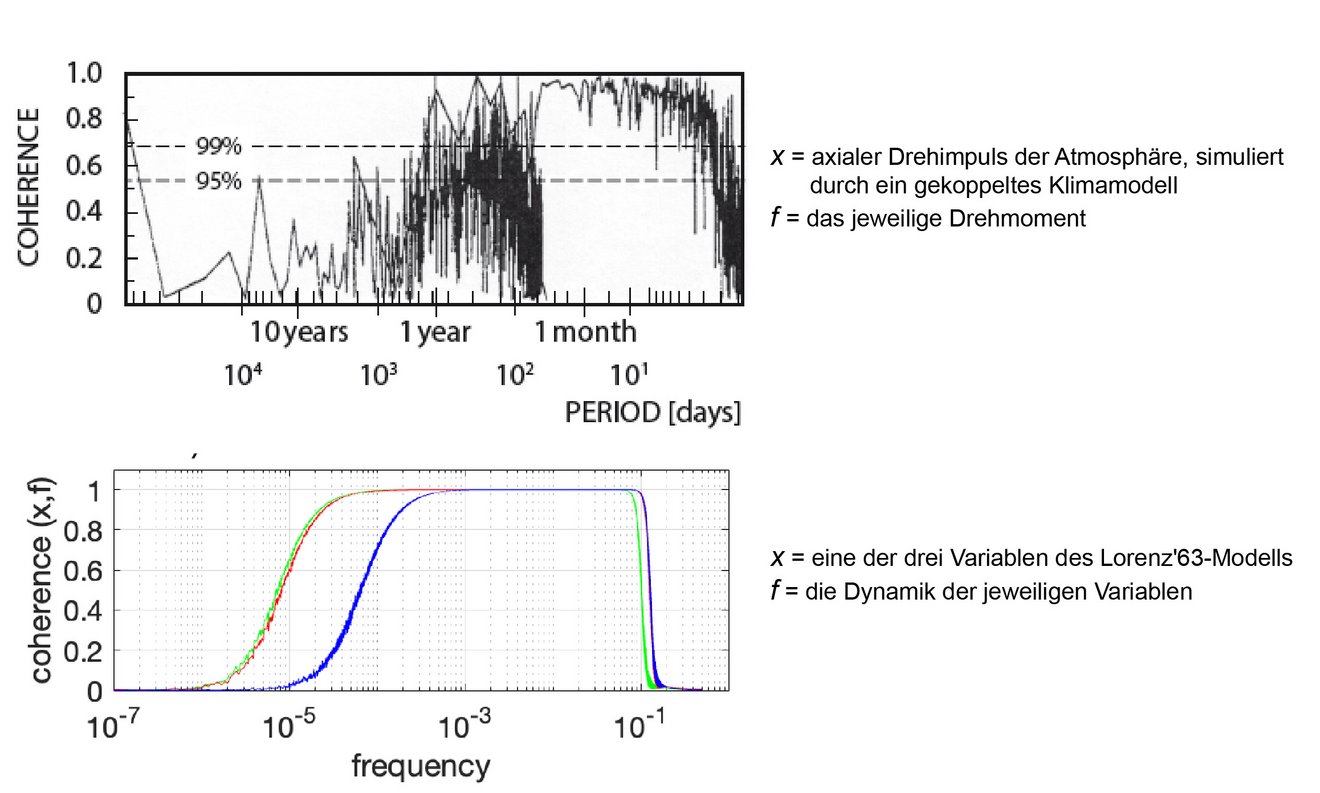
Abb.: Kohärenzspektren zwischen x and f für zwei dynamische Systeme – ein gekoppeltes Modell (oben) und das Lorenz-Modell (unten) – sowie für die erste, zweite und dritte Komponente des Lorenz-Modells (grün, rot und blau, unten). Jedes der betrachteten dynamischen Systeme wird durch einen mehrdimensionalen Zustandsvektor x beschrieben. Für das gekoppelte Modell ist x der axiale Drehimpuls der Atmosphäre und damit eine Funktion von x. Für das Lorenz-Modell ist x eine Komponente von x. In beiden Fällen ist f = f (x) die Dynamik, die die Entwicklung von x über dx / dt = f bestimmt.
Die fehlende Verbindung zwischen einer Klimavariablen x und ihrer Dynamik f auf ultralangen Zeitskalen schafft Raum für einen anderen Mechanismus zur Erzeugung von Varianz – den Integraleffekt, der stattdessen wirksam werden kann. Dieser Mechanismus kann nicht in Form von f an einzelnen Zeitpunkten ausgedrückt werden. Er entfaltet sich nur bei der zeitlichen Integration der Gleichungen und muss stochastisch dargestellt werden, z. B. in Form eines stochastischen Klimamodells von Hasselmann (Hasselmann, 1976). Ein physikalisches Phänomen wie die interne Klimavariabilität auf ultralangen Zeitskalen kann nicht durch zwei verschiedene Arten von Evolutionsgesetzen bestimmt werden, von denen das eine in Form von deterministischen Differentialgleichungen und das andere in Form von stochastischen Differentialgleichungen formuliert ist. Die Machtlosigkeit von f legt nahe, dass ein stochastisches Modell (sofern es identifiziert werden kann) nicht als Näherung betrachtet werden sollte, sondern zu etwas “aufgewertet“ werden sollte, dass denselben Status hat wie die deterministischen Evolutionsgesetze, die in Form von f dargestellt sind.
Originalveröffentlichung
von Storch, J. S. (2022). On equilibrium fluctuations. Tellus A, 74, 364-381. doi: 10.16993/tellusa.25
Literaturhinweis
Hasselmann, K. (1976). Stochastic climate models: Part 1. Theory. Tellus, 28, 473-485. doi: 10.3402/tellusa.v28i6.11316
Kontakt
Prof. Jin-Song von Storch
Max-Planck-Institut für Meteorologie
E-Mail: jin-song.von.storch@mpimet.mpg.de
