
Complex Modelling and Extreme Computing
Our goal is to understand the dynamics of the ocean and its role in the climate by combining numerical methods, physical considerations, mathematical analysis and numerical experiments. The Complex Modelling and Extreme Computing Group
- developes state-of-the-art circulation models of the ocean,
- carries out High-Performance Computations,
- develops sophisticated diagnostics to analyse the simulated circulation.
The theme of the group is located at the interface between Applied Mathematics, Scientific Computing, and Physical Oceanography and centering around the ocean model ICON-O.
Cutting-Edge Numerics
We develope structure-preserving numerical schemes that embed a physical concept into a numerical model. These methods, also known as "mimetic" or "phyiscs capturing method" intend to improve the quality of the simulations by formulating discrete equivalents of essential properties of continuum physics. This idea has been filled with life in the design and realization of the ocean general circulation model ICON-O.
Innovative Parametrizations
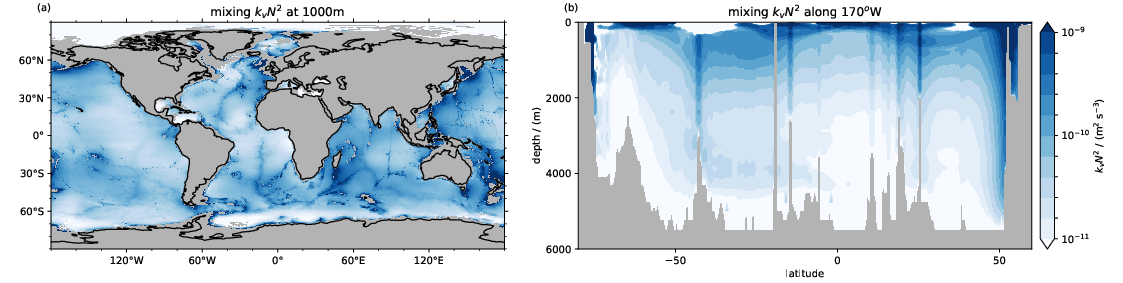
Several important processes in the ocean remain unresolved. These processes are represented in ocean models by parametrizations or Subgrid-Scale Models. For the parametrization of diapycnal mixing in the ocean, we develop and implement novel parameterizations describe energetically consistent energy pathways from surface and interior waves to small-scale turbulence. High-resolution ICON-O simulations guide us how to even better connect different energy reservoirs and to further improve the fidelity of the model.
Creative Experimental Configurations
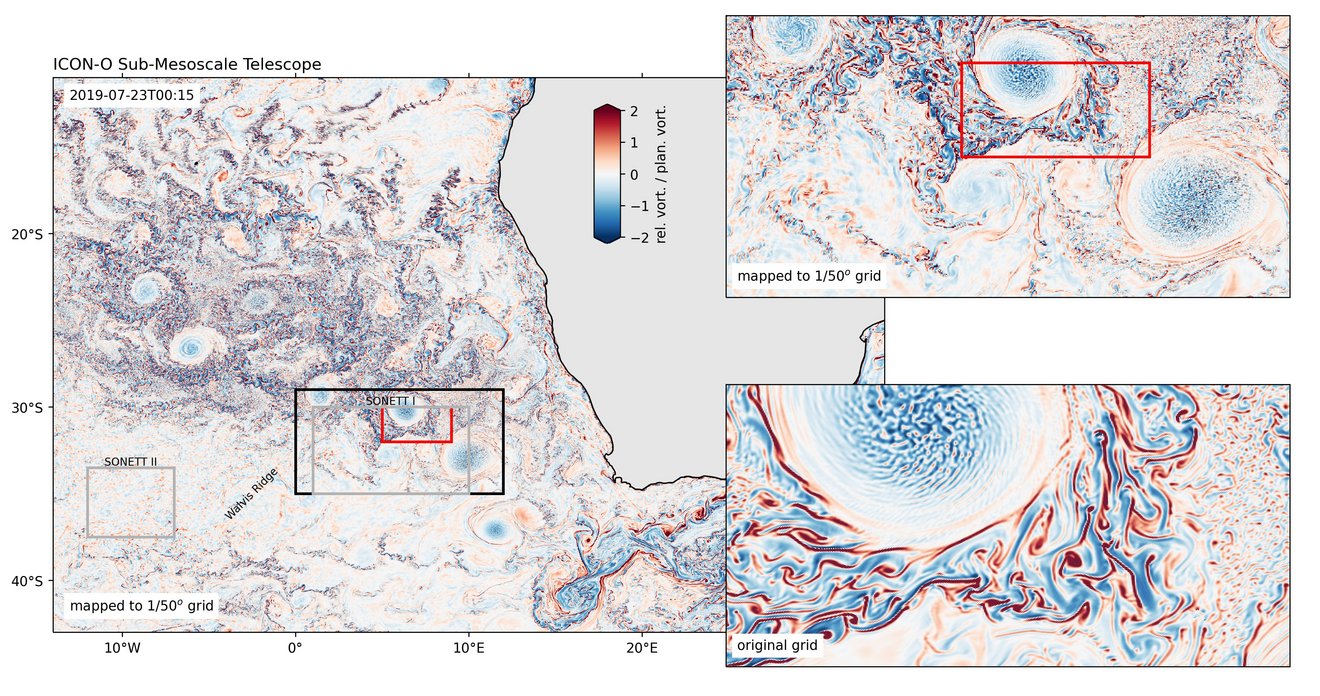
To expand the range of resolved scales we push for the possible computational limits with high-resolution simulations in ocean-stand-alone and coupled configuratins. A glance at new dynamical regimes that are beyond the actual possible resolution of global ocean models can be taken by using a *telescoping model configuration* that locally increases the resolution and allows to investigate for example submesoscale dynamics in a realsitic scenario.
Novel diagnostics
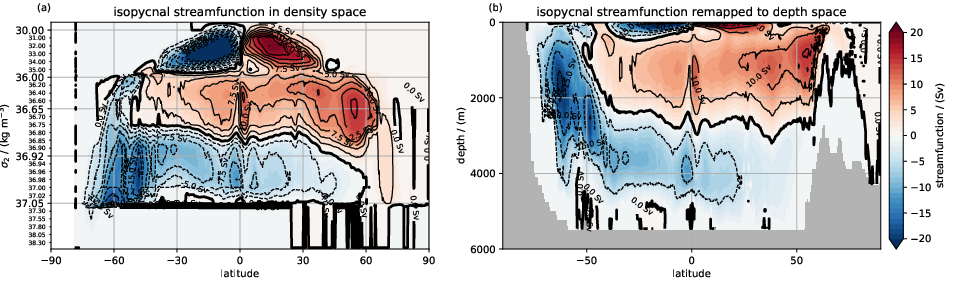
The increased spatial resolution in many of our simulations and the focus on small-scale processes goes along with a substantial increase of data which needs to be analyzed. We explore different complementary attempts to make such diagnostics possible even for our largest data sets. In this regard, we explore an increased usage of online diagnostics in particular for transport and energy exchanges.
Group members and publications
- Bastin, S., Koldunov, A., Schütte, F., Gutjahr, O., Mrozowska, M., Fischer, T., Shevchenko, R., Kumar, A., Koldunov, N., Haak, H., Brüggemann, N., Hummels, R., Specht, M., Jungclaus, J., Danilov, S., Dengler, M. & Jochum, M. (2025). Sensitivity of the tropical Atlantic to vertical mixing in two ocean models (ICON-O v2.6.6 and FESOM v2.5). Geoscientific Model Development, 18(4), 1189-1220. doi:10.5194/gmd-18-1189-2025 [publisher-version]
- Müller, W., Früh, B., Korn, P., Potthast, R., Baehr, J., Bettems, J.-M., Bölöni, G., Brienen, S., Fröhlich, K., Helmert, J., Jungclaus, J., Köhler, M., Lorenz, S., Schneidereit, A., Schnur, R., Schulz, J.-P., Schlemmer, L., Sgoff, C., Pham, T., Pohlmann, H., Vogel, B., Vogel, H., Wirth, R., Zaehle, S., Zängl, G., Stevens, B. & Marotzke, J. (2025). ICON: toward vertically integrated model configurations for numerical weather prediction, climate predictions, and projections. Bulletin of the American Meteorological Society, 106(6), E1017-E1031. doi:10.1175/BAMS-D-24-0042.1 [publisher-version]
- Nielsen, D., Chegini, F., Serra, N., Kumar, A., Brüggemann, N., Hohenegger, C. & Ilyina, T. (2025). Resolved tropical cyclones trigger CO2 uptake and phytoplankton bloom in an Earth system model simulation. EarthArXiv, . doi:10.31223/X5KF05 [Preprint] [pre-print]
- Witte, M., Lapolli, F., Freese, P., Götschel, S., Ruprecht, D., Korn, P. & Kadow, C. (2025). Dynamic deep learning based super-resolution for the shallow water equations. Machine Learning: Science and Technology, 6: 015060. doi:10.1088/2632-2153/ada19f [publisher-version]
- Brüggemann, N., Losch, M., Scholz, P., Pollmann, F., Danilov, S., Gutjahr, O., Jungclaus, J., Koldunov, N., Korn, P., Olbers, D. & Eden, C. (2024). Parameterized internal wave mixing in three ocean general circulation models. Journal of Advances in Modeling Earth Systems, 16: e2023MS003768. doi:10.1029/2023MS003768 [research-data][publisher-version]
- Korn, P. & Titi, E. (2024). Global well-posedness of the primitive equations of large-scale ocean dynamics with the Gent-McWilliams-Redi Eddy Parametrization Model. SIAM journal on mathematical analysis, 56(6), 8011-8036. doi:10.1137/23M1564316 [publisher-version]
- Lapolli, F., da Silva Peixoto, P. & Korn, P. (2024). Accuracy and stability analysis of horizontal discretizations used in unstructured grid ocean models. Ocean Modelling, 189: 102335. doi:10.1016/j.ocemod.2024.102335 [publisher-version]
- Proske, U., Brüggemann, N., Gärtner, J., Gutjahr, O., Haak, H., Putrasahan, D. & Wieners, K.-H. (2024). A case for open communication of bugs in climate models, made with ICON version 2024.01. EGUsphere, . doi:10.5194/egusphere-2024-3493 [Preprint] [pre-print]
- Ssebandeke, J. (2024). Quantifying aspects of the ocean's energetics using eddy-resolving simulations. Phd Thesis, Berichte zur Erdsystemforschung, 279. [publisher-version]
- Ssebandeke, J., von Storch, J. & Brüggemann, N. (2024). Sensitivity of the global Lorenz energy cycle. Ocean Dynamics, available online.. doi:10.1007/s10236-023-01568-6 [publisher-version][supplementary-material]
- Crisan, D., Holm, D. & Korn, P. (2023). An implementation of Hasselmann’s paradigm for stochastic climate modelling based on stochastic Lie transport. Nonlinearity, 36, 4862-4903. doi:10.1088/1361-6544/ace1ce [publisher-version]
- Hohenegger, C., Korn, P., Linardakis, L., Redler, R., Schnur, R., Adamidis, P., Bao, J., Bastin, S., Behravesh, M., Bergemann, M., Biercamp, J., Bockelmann, H., Brokopf, R., Brüggemann, N., Casaroli, L., Chegini, F., Datseris, G., Esch, M., George, G., Giorgetta, M., Gutjahr, O., Haak, H., Hanke, M., Ilyina, T., Jahns, T., Jungclaus, J., Kern, M., Klocke, D., Kluft, L., Kölling, T., Kornblueh, L., Kosukhin, S., Kroll, C., Lee, J., Mauritsen, T., Mehlmann, C., Mieslinger, T., Naumann, A., Paccini, L., Peinado, A., Praturi, D., Putrasahan, D., Rast, S., Riddick, T., Roeber, N., Schmidt, H., Schulzweida, U., Schütte, F., Segura, H., Shevchenko, R., Singh, V., Specht, M., Stephan, C., von Storch, J., Vogel, R., Wengel, C., Winkler, M., Ziemen, F., Marotzke, J. & Stevens, B. (2023). ICON-Sapphire: simulating the components of the Earth System and their interactions at kilometer and subkilometer scales. Geoscientific Model Development, 16, 779-811. doi:10.5194/gmd-16-779-2023 [publisher-version]
- Sharma, K. & Korn, P. (2023). Numerical simulation of an idealized coupled ocean-atmosphere climate model. In Iske, A. & Rung, T. (Eds.), Modeling, Simulation and Optimization of Fluid Dynamic Applications (pp.113-130). Cham: Springer Nature . doi:10.1007/978-3-031-45158-4_7
- von Storch, J.-S., Hertwig, E., Lüschow, V., Brüggemann, N., Haak, H., Korn, P. & Singh, V. (2023). Open-ocean tides simulated by ICON-O. Geoscientific Model Development, 16, 5179-5196. doi:10.5194/gmd-16-5179-2023 [supplementary-material][publisher-version][any-fulltext]
- Danilov, S., Mehlmann, C. & Fofonova, V. (2022). On discretizing sea-ice dynamics on triangular meshes using vertex, cell or edge velocities. Ocean Modelling, 170: 101937. doi:10.1016/j.ocemod.2021.101937
- Jungclaus, J., Lorenz, S., Schmidt, H., Brovkin, V., Brüggemann, N., Chegini, F., Crueger, T., de Vrese, P., Gayler, V., Giorgetta, M., Gutjahr, O., Haak, H., Hagemann , S., Hanke, M., Ilyina, T., Korn, P., Kröger, J., Linardakis, L., Mehlmann, C., Mikolajewicz, U., Müller, W., Nabel, J., Notz, D., Pohlmann, H., Putrasahan, D., Raddatz, T., Ramme, L., Redler, R., Reick, C., Riddick, T., Sam, T., Schneck, R., Schnur, R., Schupfner, M., von Storch, J.-S., Wachsmann, F., Wieners, K.-H., Ziemen, F., Stevens, B., Marotzke, J. & Claussen, M. (2022). The ICON Earth System Model Version 1.0. Journal of Advances in Modeling Earth Systems, 14: e2021MS002813. doi:10.1029/2021MS002813 [publisher-version]
- Korn, P., Brüggemann, N., Jungclaus, J., Lorenz, S., Gutjahr, O., Haak, H., Linardakis, L., Mehlmann, C., Mikolajewicz, U., Notz, D., Putrasahan, D., Singh, V., von Storch, J.-S., Zhu , X. & Marotzke, J. (2022). ICON-O: The Ocean Component of the ICON Earth System Model - Global simulation characteristics and local telescoping capability. Journal of Advances in Modeling Earth Systems, 14: e2021MS002952. doi:10.1029/2021MS002952 [publisher-version]
- Kumar, A., Brüggemann, N., Smith, R. & Marotzke, J. (2022). Response of a tropical cyclone to a subsurface ocean eddy and the role of boundary layer dynamics. Quarterly Journal of the Royal Meteorological Society, 148, 378-402. doi:10.1002/qj.4210 [publisher-version]
- Linardakis, L., Stemmler, I., Hanke, M., Ramme, L., Chegini, F., Ilyina, T. & Korn, P. (2022). Improving scalability of Earth System Models through coarse-grained component concurrency - a case study with the ICON v2.6.5 modelling system. Geoscientific Model Development, 15, 9157-9176. doi:10.5194/gmd-15-9157-2022 [publisher-version]
- Mathis, M., Logemann, K., Maerz, J., Lacroix, F., Hagemann, S., Chegini, F., Ramme, L., Ilyina, T., Korn, P. & Schrum, C. (2022). Seamless integration of the coastal ocean in global marine carbon cycle modeling. Journal of Advances in Modeling Earth Systems, 14: e2021MS002789. doi:10.1029/2021MS002789 [publisher-version]
- Korn, P. (2021). Strong solvability of a variational data assimilation problem for the primitive equations of large-scale atmosphere and ocean dynamics. Journal of Nonlinear Science, 31: 56. doi:10.1007/s00332-021-09707-3 [publisher-version]
- Korn, P. (2021). Global well-posedness of the ocean primitive equations with nonlinear thermodynamics. Journal of Mathematical Fluid Mechanics, 23: 71. doi:10.1007/s00021-021-00596-w [publisher-version]
- Krönert, L. (2021). A split-explizit time-stepping scheme for ICON-Ocean. Phd Thesis, Hamburg: Universität Hamburg. Berichte zur Erdsystemforschung, 242. doi:10.17617/2.3311083 [publisher-version]
- Logemann, K., Linardakis, L., Korn, P. & Schrum, C. (2021). Global tide simulations with ICON-O: testing the model performance on highly irregular meshes. Ocean Dynamics, 71, 43-57. doi:10.1007/s10236-020-01428-7 [publisher-version]
- Mehlmann, C., Danilov, S., Losch, M., Lemieux, J., Hutter, N., Richter, T., Blain, P., Hunke, E. & Korn, P. (2021). Simulating linear kinematic features in viscous-plastic sea ice models on quadrilateral and triangular grids with different variable staggering. Journal of Advances in Modeling Earth Systems, 13: e2021MS002523. doi:10.1029/2021MS002523 [publisher-version]
- Mehlmann , C. & Richter, T. (2020). A goal oriented error estimator and mesh adaptivity for sea ice simulations. Ocean Modelling, 154: 101684. doi:10.1016/j.ocemod.2020.101684 [pre-print]
- Singh , V. & Frankel, S. (2020). On the use of split forms and wall modeling to enable accurate high-Reynolds number discontinuous Galerkin simulations on body-fitted unstructured grids. Computers & Fluids, 208: 104616. doi:10.1016/j.compfluid.2020.104616
- Korn, P. & Linardakis, L. (2018). A conservative discretization of the shallow-water equations on triangular grids. Journal of Computational Physics, 375, 871-900. doi:10.1016/j.jcp.2018.09.002
- Korn, P. (2018). A structure-preserving discretization of ocean parametrization on unstructured grids. Ocean Modelling, 132, 73-90. doi:10.1016/j.ocemod.2018.10.002
- Korn, P. (2018). A regularity-aware algorithm for variational data assimilation of an idealized coupled atmosphere–ocean model. Journal of Scientific Computing, 79, 748-786. doi:10.1007/s10915-018-0871-y [publisher-version]
- Ackmann, J. (2017). Error estimation algorithms for ocean models. Phd Thesis, Hamburg: Universität Hamburg. Berichte zur Erdsystemforschung, 186. doi:10.17617/2.2383652 [publisher-version]
- Ackmann, J., Marotzke, J. & Korn, P. (2017). Stochastic goal-oriented error estimation with memory. Journal of Computational Physics, 348, 195-219 . doi:10.1016/j.jcp.2017.07.009
- Korn, P. (2017). Formulation of an unstructured grid model for global ocean dynamics. Journal of Computational Physics, 339, 525-552. doi:10.1016/j.jcp.2017.03.009
- Korn, P. & Danilov, S. (2017). Elementary dispersion analysis of some mimetic discretizations on triangular C-grids. Journal of Computational Physics, 330, 156-172. doi:10.1016/j.jcp.2016.10.059
- Aizinger, V., Korn, P., Giorgetta, M. & Reich, S. (2015). Large-scale turbulence modelling via alpha-regularisation for atmospheric simulations. Journal of Turbulence, 16, 367-391. doi:10.1080/14685248.2014.991443
- Rauser, F., Marotzke, J. & Korn, P. (2015). Ensemble-type numerical uncertainty information from single model integrations. Journal of Computational Physics, 292, 30-42. doi:10.1016/j.jcp.2015.02.043
- Vlasenko, A., Korn, P., Riehme, J. & Naumann, U. (2014). Estimation of data assimilation error: A shallow-water model study. Monthly Weather Review, 142, 2502-2520. doi:10.1175/MWR-D-13-00205.1
- Korn, P. (2009). Data assimilation for the Navier-Stokes-alpha equations. Physica D: Nonlinear Phenomena, 238, 1957-1974. doi:10.1016/j.physd.2009.07.008
Contact
Dr. Nils Brüggemann
Group leader
Phone: +49 (0)40 41173-153
nils.brueggemann@mpimet.mpg.de
Dr. Peter Korn
Group leader
Phone: +49 (0)40 41173-470
peter.korn@mpimet.mpg.de
More Content
Towards resolving internal tides in the ocean
In a recent publication, Prof. Jin-Song von Storch together with other scientists showed that the ocean component of the ICON model is able to…
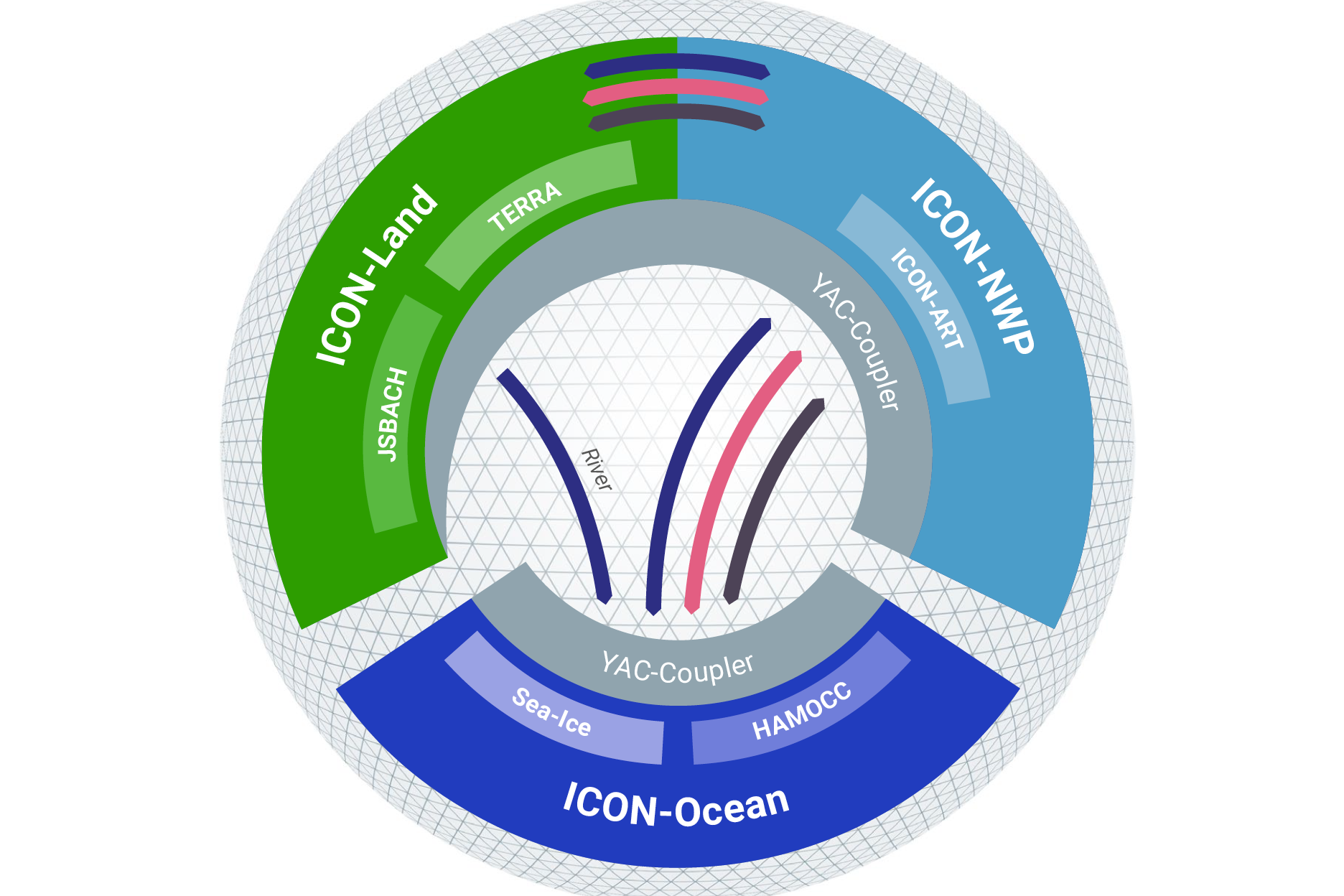
Weather forecasting and climate modeling move closer together
The ICON model can be used for weather forecasting as well as climate predictions and long-term projections. So far, however, the different…

